Тема 3.1 Числовые ряды. Сходимость рядов.

Определение. Числовым рядом называется бесконечная последовательность чисел и₁, и₂,и₃,…,и_n… соединенных знаком сложения:

и₁+и₂₊,и₃+…+и_n+…=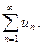

Числа и₁, и₂,и₃,…,и_n… называются членами ряда, член и_n- общим членом или n-м членом ряда.

Ряд считается заданным, если известен его общий член и_n. Например, ряд с общим членом и_n= 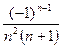имеет вид

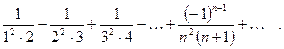
Более сложной является обратная задача: по нескольким первым членам ряда написать общий член.

Пример : Найти в простейшей форме общий член ряда:

а) 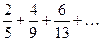б)

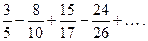
Решение : нетрудно убедиться, что для ряда а) общий член 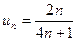, а для ряда б)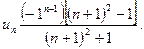

Рассмотрим суммы конечного числа членов ряда:

S₁=u₁, S₂=u₁+u₂, …, S_n=u₁+u₂+u₃+…+u_n.

Сумма n первых членов ряда S_n называется n-й частичной суммой ряда.

Определение :Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е.

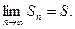
Число S называется суммойряда. В этом смысле можно записать

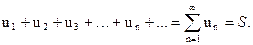
Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.

Пример : Найти сумму ряда

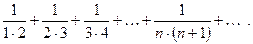
Решение : n-я частичная сумма ряда

S_n= 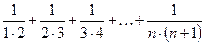.Учитывая, что

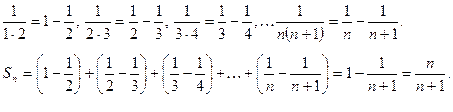
Отсюда, 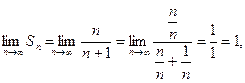т.е. сумма ряда S =1.