Тема 3.3 Ряды с положительными членами .

Теорема (признак сравнения). Пусть даны два ряда с положительными членами: 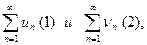причем члены первого ряда превосходят членов второго ряда, т.е. при любом n

u_{n ≤ .}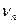

Тогда : а) если сходиться ряд (2), то сходиться и ряд(1);

б) если расходится ряд(1), то расходиться и ряд (2).

Пример . Исследовать сходимость ряда

.

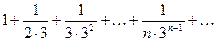Решение:

Сравним данный ряд со сходящимся геометрическим рядом

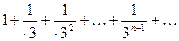( его знаменатель q= 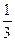<1)

Так как члены данного ряда, начиная со второго , меньше членов сходящегося геометрического ряда 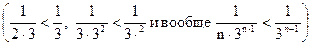, то на основании признака сравнения ряд сходиться.

Весьма удобным на практике является признак Даламбера.

Теорема (признак Даламбера).Пусть для ряда 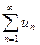с положительными членами существует предел отношения (n+1)-го члена к n-му члену 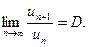Тогда, если D< 1, то ряд сходиться; если D> 1, то ряд расходиться; если D=1, то вопрос о сходимости ряда остается нерешенным.

Пример . Исследовать сходимость ряда .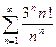

Решение:

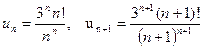. Тогда предел отношения будет равен

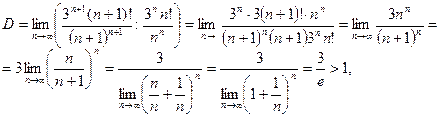
то по признаку Даламбера ряд сходиться.

Замечание 1. Если 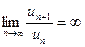, то ряд расходиться.

Замечание 2. Если 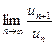=1, то признак Даламбера ответа о сходимости не дает, и рекомендуется перейти к другим признакам сравнения.