Ряды с неотрицательными членами
При изучении знакопостоянных рядов ограничимся рассмотрением рядов с неотрицательными членами, т.к. при простом умножении на –1 из этих рядов можно получить ряды с неположительными членами.
Теорема. Для сходимости ряда  с неотрицательными членами необходимо и достаточно, чтобы частичные суммы ряда были ограничены.
с неотрицательными членами необходимо и достаточно, чтобы частичные суммы ряда были ограничены.
Пусть даны два ряда  и
и 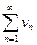 причём
причём 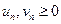 .
.
Теорема. (1-ый признак сравнения рядов с неотрицательными членами) Если 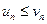 при любом n, то из сходимости ряда
при любом n, то из сходимости ряда 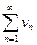 следует сходимость ряда
следует сходимость ряда  , а из расходимости ряда
, а из расходимости ряда  следует расходимость ряда
следует расходимость ряда 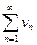 .
.
Доказательство. Обозначим через 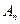 и
и 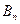 частные суммы рядов
частные суммы рядов  и
и 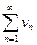 . Т.к. по условию теоремы ряд
. Т.к. по условию теоремы ряд 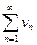 сходится, то его частные суммы ограничены, т.е. при всех n
сходится, то его частные суммы ограничены, т.е. при всех n 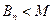 , где
, где 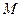 – некоторое положительное число. Но т.к.
– некоторое положительное число. Но т.к. 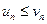 , то
, то 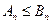 то частные суммы ряда
то частные суммы ряда  тоже ограничены, а этого достаточно для сходимости.
тоже ограничены, а этого достаточно для сходимости.
Пример. Исследовать на сходимость ряд 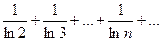
Т.к. 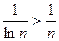 ,
, 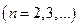 а гармонический ряд
а гармонический ряд 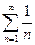 расходится (доказательство ниже), то расходится и ряд
расходится (доказательство ниже), то расходится и ряд 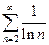 .
.
Пример. Исследовать на сходимость ряд 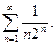
Т.к. 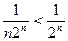 , а ряд
, а ряд 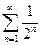 сходится (как убывающая геометрическая прогрессия), то ряд
сходится (как убывающая геометрическая прогрессия), то ряд 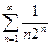 тоже сходится.
тоже сходится.
Теорема. (2-ый признак сравнения рядов с неотрицательными членами) Если 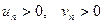 и существует предел
и существует предел 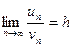 , где h – число, отличное от нуля, то ряды
, где h – число, отличное от нуля, то ряды  и
и 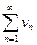 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Теорема. (Признак Даламбера) Если для ряда  с положительными членами существует такое число
с положительными членами существует такое число 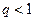 , что для всех достаточно больших n выполняется неравенство
, что для всех достаточно больших n выполняется неравенство
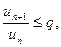
то ряд  сходится, если же для всех достаточно больших n выполняется условие
сходится, если же для всех достаточно больших n выполняется условие
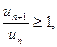
то ряд  расходится.
расходится.
Следствие. Если существует предел 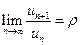 , то при
, то при 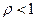 ряд сходится, а при
ряд сходится, а при 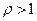 – расходится. Если
– расходится. Если 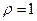 , то признак ответа не даёт.
, то признак ответа не даёт.
Пример. Определить сходимость ряда 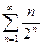 .
.
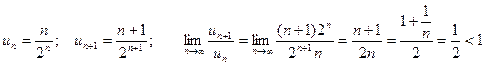 .
.
Вывод: ряд сходится.
Пример. Определить сходимость ряда 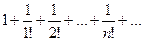
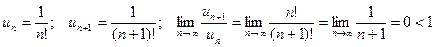 .
.
Вывод: ряд сходится.
Теорема. (Признак Коши) Если для ряда  с неотрицательными членами существует такое число
с неотрицательными членами существует такое число 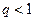 , что для всех достаточно больших n выполняется неравенство
, что для всех достаточно больших n выполняется неравенство
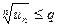 ,
,
то ряд  сходится, если же для всех достаточно больших n выполняется неравенство
сходится, если же для всех достаточно больших n выполняется неравенство
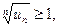
то ряд  расходится.
расходится.
Следствие. Если существует предел 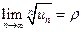 , то при
, то при 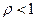 ряд сходится, а при
ряд сходится, а при 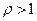 ряд расходится. При
ряд расходится. При 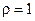 признак ответа не даёт.
признак ответа не даёт.
Пример. Определить сходимость ряда 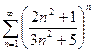 .
.
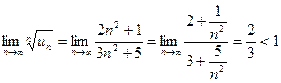 .
.
Вывод: ряд сходится.
Пример. Определить сходимость ряда 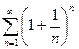 .
.
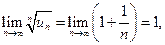
т.е. признак Коши не дает ответа на вопрос о сходимости ряда. Проверим выполнение необходимых условий сходимости. Как было сказано выше, если ряд сходится, то общий член ряда стремится к нулю.
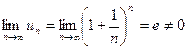 ,
,
таким образом, необходимое условие сходимости не выполняется, значит, ряд расходится.
Теорема. (Интегральный признак Коши) Если 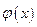 – непрерывная неотрицательная функция, убывающая на луче
– непрерывная неотрицательная функция, убывающая на луче 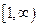 , то ряд
, то ряд 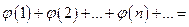
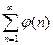 и несобственный интеграл
и несобственный интеграл 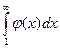 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Пример. Ряд 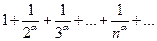 сходится при
сходится при 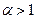 и расходится
и расходится 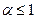 так как соответствующий несобственный интеграл
так как соответствующий несобственный интеграл 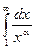 сходится при
сходится при 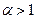 и расходится
и расходится 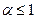 . Ряд
. Ряд 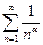 называется обобщённым гармоническимрядом.
называется обобщённым гармоническимрядом.
Дата добавления: 2015-09-29; просмотров: 960;
