Свойства числовых рядов

1) Сходимость или расходимость ряда не нарушится, если отбросить или добавить произвольное конечное число членов ряда.

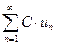2) Рассмотрим два ряда и , где С – постоянное число.

Теорема. Если ряд сходится и имеет сумму равную S, то ряд 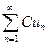также сходится, и имеет сумму равную .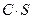

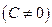3) Рассмотрим два ряда и 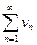. Суммой (разностью) этих рядов называется ряд 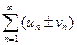, где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.

Теорема. Если ряды и 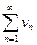сходятся и их суммы равны соответственно и 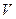, то ряд 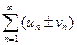тоже сходится и его сумма равна .

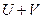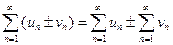
Сумма (разность) двух сходящихся рядов также является сходящимся рядом.

Сумма сходящегося и расходящегося рядов является расходящимся рядом.

О сумме двух расходящихся рядов общего утверждения сделать нельзя.

При изучении рядов решают в основном две задачи: исследование на сходимость и нахождение суммы ряда.