Знакопеременные ряды
Определение. Знакопеременным рядом называется ряд с членами произвольных знаков.
Рассмотрим знакопеременный ряд:
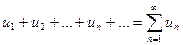 (6.1)
(6.1)
и ряд, составленный из абсолютных величин членов ряда (6.1):
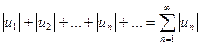 . (6.2)
. (6.2)
Теорема. Из сходимости ряда (6.2) следует сходимость ряда (6.1).
Доказательство. Ряд (6.2) является рядом с неотрицательными членами. Если ряд (2) сходится, то по критерию Коши для любого 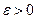 существует число N, такое, что при
существует число N, такое, что при 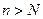 и любом целом
и любом целом 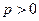 верно неравенство:
верно неравенство:
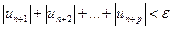
По свойству абсолютных величин:
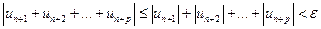

То есть по критерию Коши из сходимости ряда (6.2) следует сходимость ряда (6.1).
Определение. Ряд  называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд 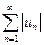 .
.
Очевидно, что для знакопостоянных рядов понятия сходимости и абсолютной сходимости совпадают.
Определение. Ряд  называется условно сходящимся, если он сходится, а ряд
называется условно сходящимся, если он сходится, а ряд 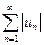 расходится.
расходится.
Теорема.Если ряд  сходится условно, то для любого наперёд заданного числа
сходится условно, то для любого наперёд заданного числа 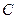 (включая
(включая 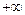 или
или 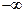 ) члены ряда можно переставить таким образом, чтобы его сумма была равна этому числу
) члены ряда можно переставить таким образом, чтобы его сумма была равна этому числу 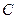 (
( 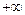 или
или 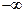 ).
).
Пусть  - знакопеременный ряд.
- знакопеременный ряд.
Теорема.(Признак Даламбера) Если существует предел 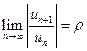 , то при
, то при 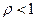 ряд
ряд  сходится абсолютно, а при
сходится абсолютно, а при 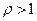 ряд расходится. При
ряд расходится. При 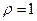 признак ответа не дает.
признак ответа не дает.
Теорема.(Признак Коши) Если существует предел 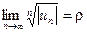 , то при
, то при 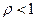 ряд
ряд  сходится абсолютно, а при
сходится абсолютно, а при 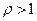 расходится. При
расходится. При 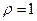 признак ответа не дает.
признак ответа не дает.
Дата добавления: 2015-09-29; просмотров: 572;
