Свойства абсолютно сходящихся рядов

Теорема. Если ряд сходится абсолютно, то ряд, полученный из него любой перестановкой членов, также сходится абсолютно и имеет ту же сумму что и исходный ряд.

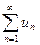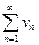Теорема. Если ряды и сходятся абсолютно и их суммы равны соответственно и 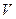, то ряд, составленный из всех произведений вида 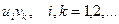взятых в каком угодно порядке, также сходится абсолютно и его сумма равна 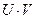- произведению сумм перемножаемых рядов.

Замечание. Если же производить перемножение условно сходящихся рядов, то в результате можно получить расходящийся ряд.