Тема 2.2 Правила вычисления производной.
1)производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, т.е.
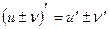
2)Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е.
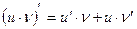
3)Производная частного двух дифференцируемых функций может быть найдена по формуле
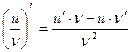(при условии, что v 
).
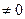Таблица производных
| № п/п | Функция у | Производная у/ | № п/п | Функция у | Функция у/ |
| с | loga u |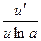 
| |||
| х | sin u | cos u.u/ | |||
| 
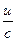
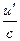
| cos u | -sin u.u/ | ||
| 
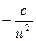
| tg u |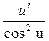 
| ||
| un | n un-1.u/ | ctg u |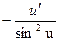 
| ||
| 
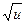
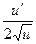
| arcsin u |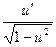 
| ||
| 
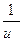
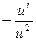
| arccos u |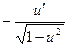 
| ||
| eu | eu.u/ | arctg u |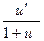 
| ||
| au | aulna.u/ | arcctg u |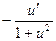 
| ||
| ln u |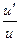 
| kx+b | k |
Упражнения :
1Вычислить производную:
№1
1) f(x)= (x+1)100; 2) f(x)= cos(6x+п); 3) f(x)= tg(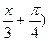 
;
4) f(x)= sin6x(x-5) ; 5) f(x)=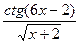 
; 6) f(x)= 
.
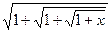№2
1) f(x)= arcos(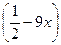 
; 2) f(x)= ln(1+sin3x); 3) f(x)= 
;
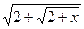4) f(x)= 43x(1+tgx); 5) f(x)=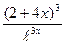 
; 6) f(x)= sin2(cos3x).
№3
1) f(x)= x3+2x-cos3x; 2) f(x)= (x+3)4; 3) f(x)= cosx3;
4) f(x)= tg6x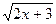 
; 5) f(x)= 
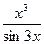; 6) f(x)= ln(6x+5)
№4
1) f(x)= 4x+5cos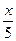 
-arcsin( 
+ 
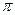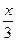); 2) f(x)= log3(2-5x);
3) f(x)= 4x+5arctg(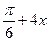 
);4) f(x)= 
;
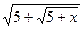5) f(x)=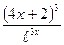 
; 6) f(x)=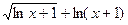 
№5
1) f(x)=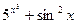 
; 2) f(x)= ln2(x+2); 3) f(x)= arcctg(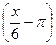 
;
4) f(x)= cos2x(5x-3)3; 5) f(x)=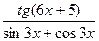 
; 6) f(x)= 
.
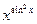2Написать уравнение касательной:
1) у= -2х2+4х-4, в точке х=3 ; 2) у=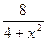 
в точке х=2;
3 Дана кривая у=х2-2х. Составить уравнение касательных в точках пересечения ее с прямой 3х+у-2=0.
Дата добавления: 2015-11-04; просмотров: 1134;