Определение и свойства последовательностей.

Множество чисел, каждое их которых снабжено своим номером, называется числовой последовательностью.

Элементы этого числового множества называются членами последовательности: х₁, х₂,х₃,…х_n,…

Чаще всего эта последовательность подчиняется какому-нибудь правилу.

Способы задания последовательностей

1) Аналитический способ задания последовательности.

Задать последовательность аналитически- это значит указать формулу, позволяющую по номеру члена последовательности однозначно определить этот член. Формула, позволяющая вычислить любой член последовательности по его номеру, называется формулой общего члена числовой последовательности.

Например, формулы общего члена

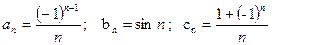
задают соответственно следующие числовые последовательности:

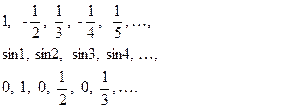
2) Рекуррентный способ задания последовательностей.

Рекуррентный способ задания состоит в том, что задается первый член( или несколько первых членов) последовательности указывается формула вычисления последующих членов последовательности по заданному первому члену( или нескольким членам).

Например, по первому члену и формуле вычисления последующих членов последовательности

a₁₌1, a_n+1=a_n+1 ,n

задается следующая последовательность:

1, 2, 3, 4, …, n-1, n, n+1, …

Последовательности бывают: ограниченные (если последовательность задается конечным числом элементов) и бесконечные ( если последовательность задается бесконечным числом элементов).

Последовательность называется монотонно возрастающей, если для любого натурального n выполнено неравенство

x_n+1>x_n.

Последовательность называется монотонно убывающей, если для любого натурального n выполнено неравенство

x_n+1<x_n.

Пример: Доказать, что последовательность, задаваемаяформулой общего члена 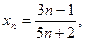возрастающая.

Решение : Рассмотрим разность

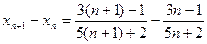и проверим выполнение неравенства для всех :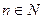

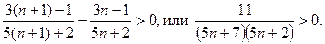
Так как последнее неравенство справедливо для всех 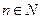, то, данная последовательность –возрастающая.