Тема 1.2 Предел числовой последовательности. Предел функции .

Вычисление пределов.

При вычислении пределов могут помочь их арифметические свойства. Пусть для последовательностей x_n и y_nсуществуют пределы 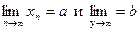. Тогда существуют пределы для суммы(разности), произведения и частного этих последовательностей, и справедливы равенства :

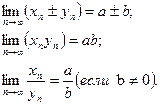
Однако воспользоваться арифметическими свойствами пределов удается далеко не всегда. Может случиться , что нет предела у одной или обеих последовательностей, но для их арифметических операций предел существует. Во всех подобных случаях говорят о неопределенностях, которые стремятся раскрыть. Существует несколько видов неопределенностей: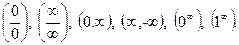

Некоторые приемы раскрытия неопределенностей.

1)Если в числителе и знаменателе дроби стоят многочлены относительно n , то при вычислении ее предела при n 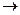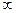полезно поделить числитель знаменатель на старшую степень n, присутствующую в многочленах.

Пример. Вычислить предел:

.

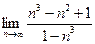Решение :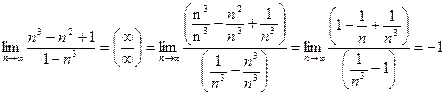

Ответ: -1

2)При вычислении предела отношений двух функций, при 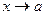, необходимо произвести сокращение числителя и знаменателя дроби на общий множитель.

Пример. Вычислить предел:

.

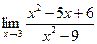Решение:

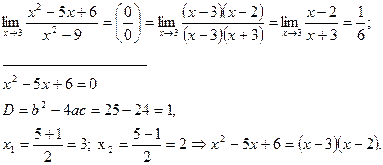
Ответ: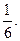

3)Вычисление предела от иррационального выражения иногда можно осуществить переводом иррациональности из числителя в знаменатель или наоборот. Для этого и числитель и знаменатель дроби, стоящей по знаком предела, надо умножить на выражение сопряженное подкоренному.

Пример. Вычислить предел:

.

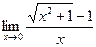Решение:

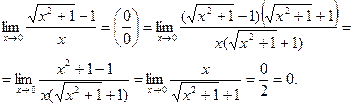
Ответ: 0.

4)При вычислении пределов выражений, содержащих тригонометрические функции, часто используется предел

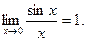
Пример . Вычислить предел:

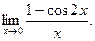
Решение :

Преобразуем, числитель дроби по формуле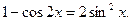

Тогда получаем

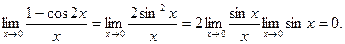
Ответ: 0.

5) Правило Лопиталя :

Предел отношения двух функций равен пределу отношения их производных, если последний существует в указанном смысле.

Пример : Вычислить предел:

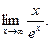
Решение :

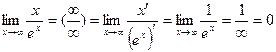
Ответ: 0.