Тема 1.3 Непрерывность функции в точке.
Ø Функция f(x), определенная на промежутке (а;b), называется непрерывной в точке х0 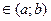 , если:
, если:
1) существует предел 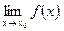 ;
;
2) этот предел равен значению функции в точке х0, т.е.
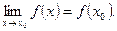
Пример : Доказать непрерывность функции
f(x)=3х2+5х, в точке х=2.
Решение:
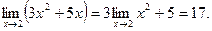
С другой стороны , значение функции в точке 2 тоже равно 17. Следовательно, равенство 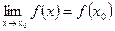 выполняется и данная функция непрерывна в точке х=2 .
выполняется и данная функция непрерывна в точке х=2 .
Ø если 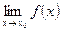 существует, но функция не определена в точке х0, то говорят, что х0- точка устранимого разрыва. В этом случае можно доопределить функцию f(x) «по непрерывности», положив
существует, но функция не определена в точке х0, то говорят, что х0- точка устранимого разрыва. В этом случае можно доопределить функцию f(x) «по непрерывности», положив
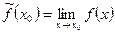 .
.
Пример . Доопределить функцию
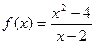 в точке х=2 по непрерывности.
в точке х=2 по непрерывности.
Решение :
точка х=2 не принадлежит области определения данной функции, но
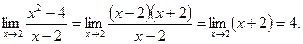
Доопределяя функцию f(x) в точке х=2 значением, равным, 4, получаем функцию
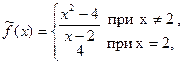
Которая на всей области определения исходной функции совпадает с исходной функцией и будет непрерывной на всей числовой оси.
Ответ : 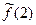 =4.
=4.
Упражнения :
Вычислить предел:
№1
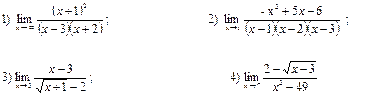
№2

 №3
№3

№4


№5

№6

Доопределить функции по непрерывности:
№1 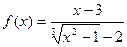 в точке х=3.
в точке х=3.
№2 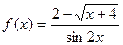 в точке х=0.
в точке х=0.
№3 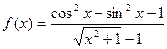 в точке х=0.
в точке х=0.

Глава 2. Математический анализ.
Дата добавления: 2015-11-04; просмотров: 1017;
