Неопределённый интеграл.

Определение. Задана 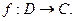Её первообразной в области D называется такая Ф, что 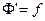в области D.

Утверждение1. Если первообразная 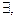то она определена с точностью до аддитивной константы.

Доказательство. Пусть 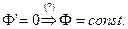(доказать).

Утверждение2. Если первообразная 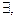то функция f – голоморфна.

Доказательство. 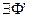=f , т.е. Ф – голоморфна 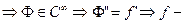голоморфна (только у голоморфной функции бывает первообразная).

Теорема3 (Теорема о существовании первообразной). Если функция f голоморфна в односвязной области D, то она имеет первообразную в этой области.

Доказательство. Рассмотрим

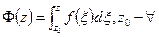фиксированная точка области, z – переменная точка. Интеграл берётся по любой спрямляемой кривой, соединяющей эти 2 точки и лежащей в области D. По интегральной теореме Коши интеграл не зависит от кривой. Докажем, что она будет первообразной.

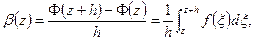
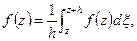
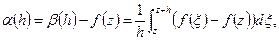надо доказать, что это 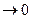. Будем

интегрировать по отрезку. Функция f непрерывна. Напишем определение непрерывности:

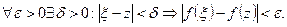
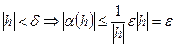, таким образом, 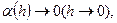т.е.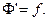

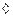
Следствие (Ньютона-Лейбница в комплексной плоскости). Если f - голоморфна в односвязной области D и Ф – первообразная, то 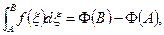интеграл берётся по любой спрямляемой кривой.

Это следствие самого доказательства теоремы.

Замечание. В многосвязной области теорема не верна.

Пример. 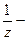голоморфна в С*. Локально первообразная 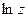определена, а глобально нет (для всего С*).

Замечание. При доказательстве теоремы3 мы пользовались только 2мя свойствами голоморфной функции: 1) непрерывность

2) интеграл по замкнутому контуру равен 0.

Дата добавления: 2015-09-02; просмотров: 875;