Первообразная и неопределённый интеграл

Обратной операцией для дифференцирования функции является нахождение её первообразной.

Первообразной для функции y= 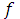(x) называется такая функция F(x),что F’(x)=f(x) для всех х из области определения f(x).

Пример:

_______________________________________________________________

Для функции у=3х² первообразной является функция F(x)=x³, а также функция F₁(x)=x³+5.

________________________________________________________________

Как видно из примера, первообразная не определяется однозначно.

Если две функции F₁(x) и F₂(x) являются первообразными для одной и той же функции 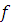(x), то их разность F₁(x)-F₂(x) = C = const (является постоянной функцией). Отсюда следует, что множество всех первообразных для данной функции 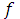(x) состоит из функций, отличающихся друг от друга на постоянную.

Неопределённым интегралом от функции 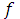(x) называется совокупность всех первообразных этой функции.

Неопределённый интеграл от функции 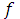(x) обозначается

.

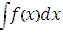Если функция F(x) является одной из первообразных для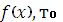

=F(x)+C.

Функция 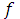(x) называется подынтегральной функцией, а выражение 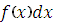подынтегральным выражением

Пример:

______________________________________________________________________________

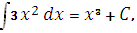
где С – произвольная постоянная. ________________________________________________________________

Достаточным условием для существования неопределённого интеграла от функции 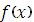является непрерывность этой функции.