Достаточные условия экстремума

ППустПусть функция y=?(x) дифференцируема в δ-окрестности точки 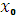. Тогда, если в этой точке производная меняет знак, имеет место локальный экстремум.

Действительно, если в левой половине δ-окрестности производная больше нуля, то в ней функция возрастает. Если при этом в правой половине δ-окрестности производная меньше нуля, то в ней функция убывает. Таким образом, если в стационарной точке 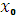производная функции меняет знак с плюса на минус, то 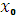является точкой максимума. Точно так же если производная меняет знак с минуса на плюс, то 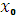- точка минимума (рис. 4.9).

– + + –

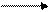
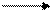
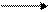
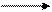min max

Рис. 4.9