Возрастание и убывание функции. Экстремумы функции
Функция y=?(x) называется возрастающей (убывающей) на промежутке X, если для любых 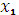 ,
, 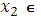 X,
X, 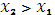 , верно неравенство
, верно неравенство
?( 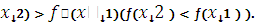
Сформулируем достаточные условия возрастания и убывания функции.
| Если производная дифференцируемой функции положительная (отрицательная) внутри некоторого промежутка X, то функция возрастает (убывает) на этом промежутке. |
Точкой максимума функции y=?(x) называется такая точка 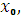 что в некоторой окрестности точки
что в некоторой окрестности точки 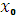 выполняется неравенство
выполняется неравенство
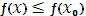 .
.
Точкой минимума функции y=?(x) называется такая точка 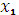 , что в некоторой окрестности точки
, что в некоторой окрестности точки 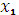 выполняется неравенство
выполняется неравенство
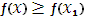 .
.
Максимумом и минимумом функции называются значения функции в точках 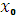 (точка максимума) и
(точка максимума) и 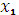 (точка минимума). Максимум и минимум функции объединяются общим названием экстремума функции.
(точка минимума). Максимум и минимум функции объединяются общим названием экстремума функции.
На рисунке 4.7 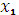 ,
, 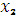 ,
, 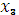 ,
, 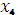 – точки экстремумов функции, а m и M – ее наименьшее и наибольшее значения.
– точки экстремумов функции, а m и M – ее наименьшее и наибольшее значения.
Следует заметить, что определенные выше максимум и минимум функции не обязательно являются ее наибольшим и наименьшим значениями на отрезке 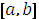 , в связи с чем они называются локальными максимумами и минимумами. Локальных максимумов и минимумов может быть много, в то время как наибольшее и наименьшее значения функции равны конкретным числам M и m.
, в связи с чем они называются локальными максимумами и минимумами. Локальных максимумов и минимумов может быть много, в то время как наибольшее и наименьшее значения функции равны конкретным числам M и m.
 y
y


 M
M

 |  |
 m
m


0a x1 x2 x3 x4b x
Рис. 4.7
Дата добавления: 2015-09-28; просмотров: 854;
