Необходимое условие экстремума
Если в точке 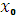 дифференцируемая функция y=?(x) имеет экстремум, то производная функции в этой точке равна нулю, т.е.
дифференцируемая функция y=?(x) имеет экстремум, то производная функции в этой точке равна нулю, т.е. 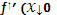 ) = 0.
) = 0.
Функция может иметь экстремум и в точках, в которых она не дифференцируема. Так, например, функция y = 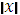 имеет экстремум (минимум) в точке x = 0, но не дифференцируема в ней (рис. 4.8, a). Функция y =
имеет экстремум (минимум) в точке x = 0, но не дифференцируема в ней (рис. 4.8, a). Функция y = 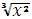 также имеет в точке x = 0 минимум (рис. 4.8, б), но производная ее в этой точке не существует. Поэтому необходимое условие экстремума может быть сформулировано следующим образом.
также имеет в точке x = 0 минимум (рис. 4.8, б), но производная ее в этой точке не существует. Поэтому необходимое условие экстремума может быть сформулировано следующим образом.
Для того, чтобы функция y=?(x) имела экстремум в точке 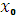 , необходимо, чтобы ее производная в этой точке равнялась нулю или не существовала, т.е. чтобы точка , необходимо, чтобы ее производная в этой точке равнялась нулю или не существовала, т.е. чтобы точка 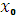 была критической. была критической.
|
Это условие не является достаточным, что показывает пример, приведенный на рис. 4.8, в.
 a б в
a б в

y = 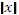









 1 y =
1 y = 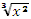 -----------------
-----------------
 |  |  |
 х х х
х х х


Рис. 4.8
Дата добавления: 2015-09-28; просмотров: 575;
