Вопрос 3. Общее условие максимизации прибыли.

Сейчас у нас уже достаточно знаний, чтобы определить условия равновесия, которые позволят монополисту максимизировать прибыль. Как следует поступить монополис­ту, если при заданной функции спроса он хотел бы максимизировать валовую прибыль (ТР)? По определению, валовая шмбыль равна разнице между общим доходом и общими издержками: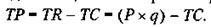

Чтобы максимизировать прибыль, предприятие должно определить равновесные цену и объем выпуска, Р* и а*, при которых совокупная прибыль была бы самой большой (раз­ность TR и производства максимальна). Обратите внимание: прибыль будет максималь­ной при таком объеме производства, при котором предельный доход предприятия равен его предельным издержкам.

Первый способ определить этот фактор максимизации прибыли — использовать таблицу издержек и доходов, такую как табл. 9.5. Чтобы найти количество и цену, при которых при­быль будет максимальной, подсчитаем значения валовой прибыли в колонке (5). Как видим, оптимальное количество — четыре единицы при цене 120 долл. за штуку. Общий доход при этом составит 480 долл., а после вычитания общих издержек в размере 250 долл. получаем, что валовая прибыль равна 230 долл. Еще раз взглянув на таблицу, убедимся, что никакая другая комбинация цена-количество не даст столь же высокий уровень валовой прибыли.

Второй, и в общем-то равноценный, способ ответить на заданный вопрос — сравнить пре­дельный доход из колонки (6) и предельные издержки из колонки (7). Пока доход, получа­емый от производства дополнительной единицы, превышает издержки ее производства, т.е. до тех пор, пока MR больше МС, прибыль предприятия увеличивается. Следовательно, оно должно продолжать наращивать производство, пока MR не достигнет МС. Для сравнения сделаем допущение, что при данном уровне производства MR меньше МС. Из этого следу­ет, что рост объема производства приводит к снижению прибыли, так что максимизирующее прибыль предприятие должно сократить объем производства. Очевидно, что прибыль макси­мальна в точке, где предельный доход равен предельным издержкам, что и видно из табл. 9.5.

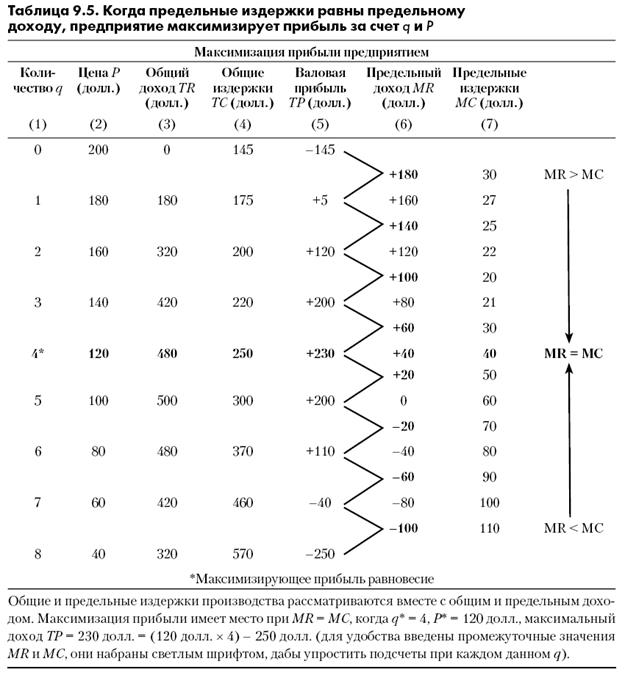
Максимизирующее прибыль равновесие

Общие и предельные издержки производства рассматриваются вместе с общим и предельным дохо­дом. Максимизация прибыли имеет место при MR = МС, когда q* = 4, Р* = 120 долл., максимальный доход ТР = 230 долл. = (120 долл. х 4) - 250 долл. (для удобства введены промежуточные значения MR и МС, они набраны светлым шрифтом, дабы упростить подсчеты при каждом данном q).

Приведенные примеры подтверждают логичность правила максимизации прибыли МС = MR, однако мы всегда стремимся понять сам принцип. Давайте еще раз посмот­рим на табл. 9.4 и предположим, что монополист выпускает q = 2. В этой точке MR от производства одной дополнительной единицы составит +100 долл., а МС равны 20 долл. Получается, что с производством дополнительной единицы предприятие должно полу­чить дополнительную прибыль MR - МС =100 долл. - 20 долл. = 80 долл. И действи­тельно в колонке (5) табл. 9.4 показано, что при увеличении производства с двух до трех единиц прирост прибыли как раз и составит 80 долл.

Отсюда следует, что, когда MR превышает МС, увеличение производства может принести дополнительную прибыль; когда МС превышают MR, прибыль можно увеличить путем сни­жения объема производства q. И только при MR = МС предприятие максимизирует прибыль, поскольку при таком соотношении нельзя увеличить прибыль, изменяя объем производства.