Вопрос 2. Чистый денежный поток, приведенная (дисконтированная) стоимость, внутренняя норма доходности.

Чистый денежный поток – разность между суммами поступлений и выплат денежных средств компании за определенный период времени. Чистый денежный поток рассчитывается с учетом выплат, дивидендов и налогов.

Понятие чистого денежного потока (Net Cash Flow, NCF) используется при оценке эффективности инвестиций. Это суммарный поток, включающий все платежи проекта, кроме платежей, связанных с притоком и оттоком капитала (при этом, например, проценты по кредитам включаются в NCF, т.к. это затраты на обеспечение проекта, а дивиденды – не включаются, т.к. это изъятие части капитала владельцами бизнеса).

В некоторых случаях, в зависимости от целей расчетов, начальные инвестиции также не включают в NCF, тогда чистый денежный поток состоит только из разности текущих поступлений и затрат, связанных с реализацией инвестиционного проекта.

Чистые денежные поступления (ЧДП), или чистый денежный поток, которые остаются у предприятия после уплаты налогов, можно в общем виде рассчитать по формуле

ЧПД= П - О, (3.1)

где П - приток денежных средств;

О - отток денежных средств.

Рис. 3.3. Схема притоков и оттоков денежных средств предприятия

Чистые денежные поступления от хозяйственной деятельности (ЧДП0) можно выразить уравнением

ЧДП0 = Вр - (И - А) - Н - Пр , (3.2)

где Вр - выручка от реализации продукции;

И - издержки производства и сбыта;

А - амортизация;

Н - налоги;

Пр - выплаты процентов по кредитам.

Амортизация по своей экономической природе, являясь отчислением, призванным обеспечить накопление средств для компенсации износа основного капитала, не перестает быть собственностью предприятия, хотя и вычитается из его прибыли. Поэтому вполне логично включать начисленную амортизацию в денежный поток (денежные поступления).

Чистый дисконтированный доход (чистая приведённая стоимость) (англ. Net present value, общепринятое сокращение — NPV (ЧДД)) — это сумма дисконтированных значений потока платежей, приведённых к сегодняшнему дню.

Иначе говоря, для потока платежей CF, где CFt — платёж через t лет (t = 1,...,N) и начальной инвестиции в размере IC = − CF0 чистый дисконтированный доход NPV рассчитывается по формуле:

,

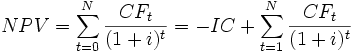где i — ставка дисконтирования.

Расчёт ЧДД — стандартный метод оценки эффективности инвестиционного проекта и показывает оценку эффекта от инвестиции, приведённую к настоящему моменту времени с учётом разной временно́й стоимости денег. Если ЧДД больше 0, то инвестиция прибыльна, а если ЧДД меньше 0, то инвестиция убыточна.

С помощью ЧДД можно также оценивать сравнительную эффективность альтернативных вложений (при одинаковых начальных вложениях более выгоден проект с наибольшим ЧДД).

В отличие от показателя дисконтированной стоимости при расчете чистого дисконтированного дохода не учитывается начальная инвестиция. Поэтому формула чистого дисконтированного дохода отличается от формулы дисконтированной стоимости на величину начальной инвестиции IC = − CF0.

Достоинства и недостатки

Положительные качества ЧДД:

- чёткие критерии принятия решений

- показатель учитывает стоимость денег во времени (используется коэффициент дисконтирования в формулах).

Отрицательные качества ЧДД: показатель не учитывает риски.

Хотя все денежные потоки (коэффициент дисконтирования может включать в себя инфляцию, однако зачастую это всего лишь норма прибыли, которая закладывается в расчетный проект) являются прогнозными значениями, формула не учитывает вероятность исхода события.

Дисконтированная стоимость выражает стоимость будущих потоков платежей в значении текущих потоков платежей. Определение дисконтированной стоимости широко используется в экономике и финансах как инструмент сравнения потоков платежей, получаемых в разные сроки. Модель дисконтированной стоимости позволяет определить какой объем финансовых вложений намерен сделать инвестор для получения определенного денежного потока через заданный срок. Дисконтированная стоимость будущего потока платежей является функцией:

- инфляции,

- срока через который ожидается будущий поток платежей,

- риска связанного с данным будущим потоком платежей,

- стоимости денег с учетом фактора времени

- других факторов.

Показатель дисконтированной стоимости используется в качестве основы для вычисления амортизации финансовых заимствований.

Объяснение

Ценность денежных средств изменяется со временем. 100 рублей, полученные через пять лет, имеют иную (в большинстве случаев, меньшую) ценность чем 100 рублей, которые имеются в наличии. Имеющиеся в наличии денежные средства можно инвестировать в банковский депозит или любой другой инвестиционный инструмент, что обеспечит процентный доход. То есть 100 руб. сегодня, дают 100 руб. плюс процентный доход через пять лет. Кроме того, на имеющиеся в наличии 100 руб. можно приобрести товар, который через пять лет будет иметь более высокую цену вследствие инфляции. Следовательно 100 руб. через пять лет не позволят приобрести тот же товар. В данном примере показатель дисконтированной стоимости позволяет вычислить сколько на сегодняшний день стоят 100 руб. которые будут получены через пять лет.

Вычисление

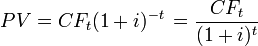
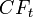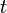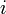где - поток платежей полученный через лет, - ставка дисконтирования определенная исходя из вышеперечисленных факторов, 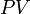- дисконтированная стоимость будущего потока платежей .

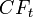Для того чтобы получить через 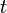лет сумму равную 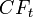, при том что инфляция, риск и др. определяют ставку дисконтирования равную 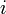, инвестор согласен вложить сегодня сумму равную .

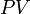В табличных процессорах в состав финансовых функций входит функция для вычисления дисконтированной стоимости. В OpenOffice.org Calc для вычисления дисконтированной стоимости различных видов платежей применяется функция PV.

Дисконтированная стоимость серии потоков платежей и аннуитетных платежей

Дисконтированная стоимость серии потоков платежей равна сумме дисконтированных стоимостей каждого из составляющих потоков платежей. Так, дисконтированная стоимость серии потоков платежей 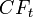получаемых каждый год в течение периода 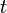лет вычисляется по следующей формуле:

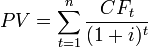
Если аннуитетные платежи имеют одинаковую величину, то эту формулу можно применять и для вычисления дисконтированной стоимости аннуитетных платежей.

Для большого 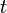, формулу можно упростить посредством сложения геометрических рядов[1]. Каждый член геометрического ряда является дисконтированной стоимостью очередного аннуитетного платежа. Дисконтированная стоимость одинаковых по величине аннуитетных платежей вычисляется по формуле:

,

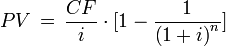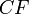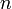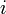где - аннуитетный платеж осуществляемый раз, - ставка дисконтирования, 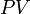- дисконтированная стоимость аннуитетных платежей .

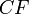Дисконтированная стоимость аннуитетных платежей с ростом

Если денежные потоки аннуитетных платежей растут в (1+g) раз (ставка роста равна g), то их дисконтированная стоимость вычисляется по формуле:

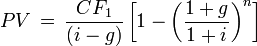
где 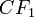- аннуитетный платеж осуществляемый в первый период, 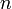- число периодов, 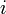- ставка дисконтирования, 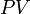- дисконтированная стоимость аннуитетных платежей.

Формула получается вычитанием формулы для расчета дисконтированной стоимости перпетуитета начинающегося в году n из упрощенной формулы модели Гордона.

Дисконтированная стоимость перпетуитетов (бессрочных аннуитетов)

Исходя из формулы расчета дисконтированной стоимости аннуитетных платежей, можно получить формулу для дисконтированной стоимости перпетуитетов(бессрочных аннуитетов). Когда значение 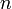стремится к бесконечности, часть формулы 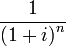, стремится к нулю. При таких условиях формула для перпетуитетов будет иметь следующий вид:

.

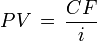Дисконтированная стоимость бессрочных ценных бумаг с растущими платежами, например акции c увеличивающимися дивидендными доходами рассчитывается по модели Гордона

Модель Гордона является вариацией модели дисконтирования дивидендов, методом для вычисления цены акции или бизнеса. Данная модель часто используется для оценки стоимости внебиржевых компаний, которую сложно оценить другими методами.

Модель подразумевает, что компания на сегодняшний день выплачивает дивиденды в размере D, которые в будущем будут увеличиваться с неизменной ставкой g. Также подразумевается, что требуемая процентная ставка (ставка дисконтирования) акции остается постоянной на уровне k.

Тогда текущая цена акции будет равна:

.

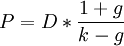На практике P часто корректируется с учетом различных факторов, например, размера компании. Распространено использование упрощенного вида формулы

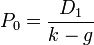
где D1 - дивиденд будущего года D1 = D0(1 + g).

Вывод формулы

Цену акции можно определить методом дисконтирования в следующем виде: .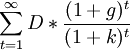

Пусть

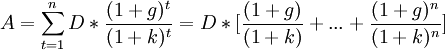
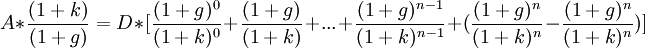
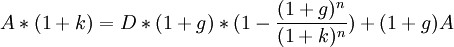
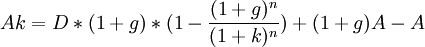
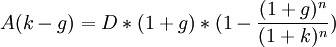
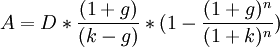
и

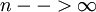и g < k

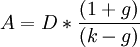
Внутренняя норма доходности (англ. internal rate of return, общепринятое сокращение — IRR (ВНД)) — это процентная ставка, при которой чистый дисконтированный доход (NPV) равен 0. NPV рассчитывается на основании потока платежей, дисконтированного к сегодняшнему дню.

Иначе говоря, для потока платежей CF, где CFt — платёж через t лет (t = 1,...,N) и начальной инвестиции в размере IC = − CF0 внутренняя норма доходности IRR рассчитывается из уравнения:

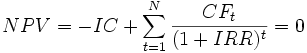
или

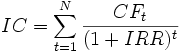
В табличных процессорах в состав финансовых функций входит функция для вычисления внутренней нормы доходности. В OpenOffice.org Calc для вычисления внутренней нормы доходности применяется функция IRR.

Пример:

Год Поток платежей

0 -100

1 +120

Расчет NPV:

i = процентная ставка

NPV = -100 +120/[(1+i/100)^1]

Расчет IRR (в процентах):

NPV = 0

-100 +120/[(1+IRR/100)^1] = 0

IRR = 20

При принятии инвестиционных решений ВНД используется для расчета ставки альтернативных вложений. При выборе из нескольких проектов с разными ВНД, выбирается проект с максимальным значением ВНД.

Внутренняя норма доходности финансовых инструментов

Внутренней доходностью для финансовых инструментов называют процентную ставку, при которой приведенная стоимость будущего потока платежей по данному финансовому инструменту совпадает с его рыночной ценой. Определённая таким образом внутренняя доходность равна внутренней норме доходности инвестиции в данный финансовый момент времени.

Для определения внутренней нормы доходности облигации часто используют приближённую «купеческую» формулу: ,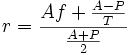

где

A — номинал облигации;

P — текущая рыночная цена облигации;

f — годовая купонная ставка;

T (в годах) — срок до погашения облигации.

Связь способа расчета внутренней нормы доходности с показателем дисконтированной стоимости состоит в том, что показатель внутренней нормы доходности отражает тот уровень ставки дисконтирования, при которой дисконтированная стоимость полученных доходов за вычетом суммы первоначальной инвестиции (чистая дисконтированная стоимость) будет равна нулю. Чем выше должна быть ставка дисконтирования для приведения чистой дисконтированной стоимости полученных доходов к нулю, тем предпочтительнее данная инвестиция.

Показатель внутренней нормы доходности основывается на допущении, что денежные потоки, полученные до погашения инвестиции (истечения срока ее действия), будут реинвестированы по ставке, равной внутренней норме доходности, и что она останется неизменной.

Инвестиция считается приемлемой, если внутренняя норма доходности выше, чем минимальный приемлемый показатель окупаемости инвестиций в финансовый инструмент. Такие инвестиции представляют интерес для инвестора.

Показатель внутренней нормы доходности для облигаций называется доходностью к погашению. Доходность к погашению облигации может отличаться от купонной ставки, если облигация продается по цене, отличающейся от номинальной стоимости.