Определённый интеграл

Пусть функция y = f(x) определена на отрезке [a,b]. Разобьём отрезок [a,b] на n частей точками 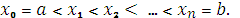На каждом из полученных отрезков [ 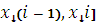(i=1,2,…, n) возьмем некоторую точку

Интегральной суммой функции y = f(x) на отрезке [a,b] называется сумма

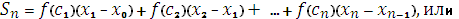
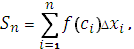
где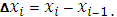

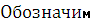наибольшую из длин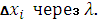

Определённым интегралом функции y = f(x) на отрезке [a,b], который обозначается

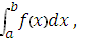называется предел интегральных сумм

(*)

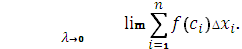Таким образом,

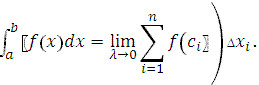
Интегрируемой называется функция, для которой существует предел, обозначенный (*). Из условия 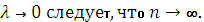Числа a и bназываются пределами интегрирования. Функция f(x) носит название подынтегральной функции.

Если функция y=f(x) непрерывна на отрезке [a,b], то определённый интеграл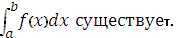

Пример:

______________________________________________________________

Пусть y=A – постоянная функция на отрезке [a,b]. Тогда интегральная сумма имеет вид:

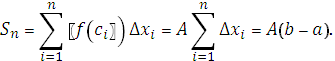
Она зависит от способа разбиения отрезка на части и

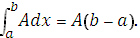
Полученное число равно площади заштрихованного прямоугольника на рис. 4.10.

у

A

0 a b x

Рис 4.10.

________________________________________________________________