Основные комбинации и формулы для их подсчета
Основными комбинациями, рассматриваемыми в комбинаторике, являются комбинации без повторений и с повторениями. Это перестановки, размещения и сочетания.
Пусть некоторое множество Х состоит из п элементов. Будем переставлять элементы этого множества всевозможными способами, оставляя неизменным их число и меняя лишь их порядок. Каждая из полученных комбинаций (в том числе и первоначальная) носит название перестановки. Общее число перестановок из п элементов обозначается Рп и вычисляется по формуле:
Рп=п!=1·2·3·…·(п-1)·п,
где п!(«эн факториал») – это произведение всех натуральных чисел от 1 до п, т.е. n! = 1· 2 · 3 ·...· n. Следует отметить, что 0!=1.
Каждое упорядоченное подмножество n-элементного множества Х, состоящее из k элементов, называется размещением из n элементов по k элементов. Через Ankобозначают число всех размещений из п элементов по k (читается: «A из n пo k»). Для числа размещений справедлива формула:
Ank =  n(n - 1)(n - 2)...(n - (k - 1)).
n(n - 1)(n - 2)...(n - (k - 1)).
Кортеж длины k, составленный из элементов n-элементного множества Х, называют размещением с повторениями из n элементов по k. Число таких кортежей обозначают  вычисляют по формуле:
вычисляют по формуле:
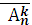 =nk.
=nk.
Сочетанием из n элементов по k элементовназывается каждое неупорядоченное k-элементное подмножество множества Х, состоящего из п элементов. Число всех сочетаний из п элементов по к элементов обозначается 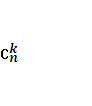 («С («цэ») из п по k»). Для числа сочетаний справедливы формулы:
(«С («цэ») из п по k»). Для числа сочетаний справедливы формулы:
 ==
== 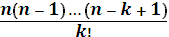 .
.
Примеры:
_____________________________________________________________________________
1. Пусть в группе 25 студентов. Сколькими способами могут быть выбраны из этой группы три делегата на конференцию?
Последовательность выбора делегатов не играет роли, поэтому здесь необходимо составить из имеющихся 25 элементов множества студентов различные трехэлементные подмножества. Это сочетания из 25 по 3:
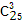 =
= 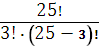 =
= 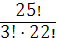 =
= 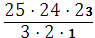 = 2300.
= 2300.
2. Сколько существует способов распределения призовых мест на олимпиаде среди 25 участников? Необходимо составить различные упорядоченные трехэлементные подмножества из элементов 25-элементного множества. Это размещения без повторений из 25 по 3:
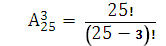 = = 25·24·23= 13800.
= = 25·24·23= 13800.
3. Сколькими способами можно составить список из 25 студентов?
В задаче необходимо найти число различных упорядоченных множеств из 25 элементов, т.е. число перестановок из 25 элементов:
Р25=25!
4. Сколькими способами группе студентов из 25 человек могут быть выставлены экзаменационные оценки в ведомости, если известно, что неудовлетворительной оценки не получил никто?
Все удовлетворительные оценки – это 4, 5, 6, 7, 8, 9, 10. Их семь. Значит, необходимо составить различные кортежи длины 25 из элементов семиэлементного множества. Число таких кортежей – это число размещений с повторениями из семи элементов по 25:
 = 725.
= 725.
______________________________________________________ __
Дата добавления: 2015-09-28; просмотров: 1210;
