Правила дифференцирования основных элементарных функций
Изучаемый материал: основные правила дифференцирования и техника дифференцирования степенных, тригонометрических, обратных тригонометрических и логарифмических функций.
Пример 1: Найти производную функции у=5х3-2х+ 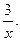
Решение: Данная функция есть алгебраическая сумма функций.
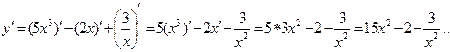
Пример 2: Найти производную функции 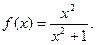
Решение: 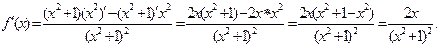
Пример 3: Найти производную функции у=sin3j и вычислить ее значение при j=p/3.
Решение: Это сложная функция с промежуточным аргументом sinj.
f¢ (j) = 3 sin2j (sin j)¢=3 sin2 j cos j.
Вычислим значение производной при j=p/3:
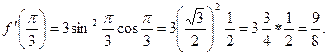
Пример 4: Найти производную функции 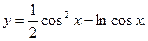
Решение: Это сложная функция с промежуточным аргументом cos х.
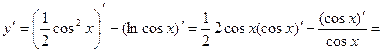
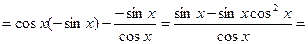
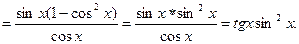
Пример 5: Найти производную функции 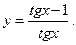
Решение: 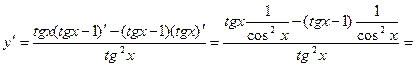
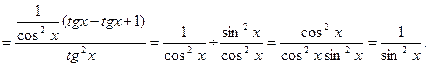
Пример 6: Найти производную функции 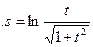 и вычислить ее значение при t=2.
и вычислить ее значение при t=2.
Решение: Сначала преобразуем функцию, используя свойства логарифмов:
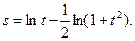
Теперь дифференцируем по формулам:
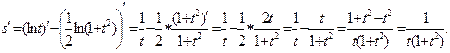
Вычислим значение производной при t=2:
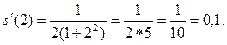
Дата добавления: 2015-10-13; просмотров: 901;
