Неравномерное движение. Ускорение

Если скорость тела (материальной точки) с течением времени изменяется по величине или направлению, то такое движение называется неравномерным. Векторная физическая величина, определяющая быстроту изменения скорости по модулю и направлению, называется ускорением. Среднее ускорение за промежуток времени Δt:

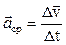, (1.1)

где 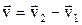- изменение вектора скорости за время Δt.

Переходя к пределу в формуле (1.1), получаем выражение для мгновенного ускорения:

.

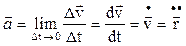Вектор ускорения может быть выражен следующими способами:

· в виде суммы составляющих по осям координат

,

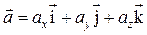где 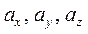− проекции вектора ускорения на соответствующие оси;

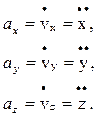
· в виде суммы взаимно перпендикулярных векторов тангенциального (касательного) и нормального ускорений (здесь мы ограничиваемся случаем плоского движения, при котором все точки траектории лежат в одной плоскости – (рис.1.3)

,

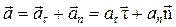где 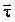– единичный вектор, сонаправленный с вектором скорости, т.е. по касательной к траектории; 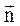– единичный вектор, направленный к центру кривизны траектории, т.е. перпендикулярно к 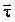. Тангенциальное ускорение характеризует быстроту изменения модуля скорости:

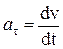. (1.2)

Нормальное ускорение характеризует быстроту изменения скорости по направлению. Его модуль:

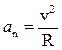, (1.3)

где R – радиус кривизны траектории в данной точке. Модуль полного ускорения равен

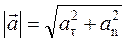. (1.4)

Разным сочетаниям тангенциального и нормального ускорений соответствуют различные виды плоского движения, приведенные в табл.1.

Таблица 1

Виды плоского движения

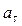
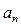
		Вид движения
		Прямолинейное равномерное
const		Прямолинейное равнопеременное
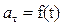
		Прямолинейное неравномерное
	const	Равномерное по окружности
	≠ 0	Криволинейное равномерное
const	≠ 0	Криволинейное равнопеременное
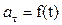
	≠ 0	Криволинейное неравномерное