Связь между линейными и угловыми величинами
Обратимся к рис. 1.4 и формуле (1.9). Для того чтобы связать линейную скорость 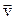 произвольной точки А твердого тела с угловой скоростью
произвольной точки А твердого тела с угловой скоростью 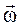 вращения этого тела вокруг неподвижной оси ОО’, поделим обе части формулы на
вращения этого тела вокруг неподвижной оси ОО’, поделим обе части формулы на 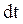 . Учитывая, что
. Учитывая, что 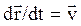 и
и 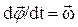 , получим
, получим
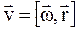 , (1.10)
, (1.10)
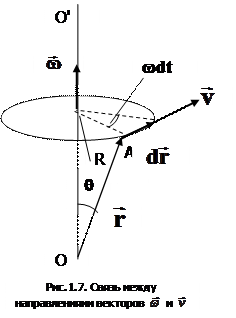 т.е. линейная скорость вращающейся точки равна векторному произведению угловой скорости на радиус-вектор этой точки (рис.1.7). Модуль вектора (1.10) равен
т.е. линейная скорость вращающейся точки равна векторному произведению угловой скорости на радиус-вектор этой точки (рис.1.7). Модуль вектора (1.10) равен 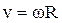 , где
, где 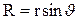 – радиус окружности, по которой движется точка А. Подставляя это выражение в формулы (1.2) и (1.3), получим
– радиус окружности, по которой движется точка А. Подставляя это выражение в формулы (1.2) и (1.3), получим 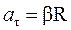 и
и 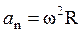 , откуда модуль полного ускорения согласно (1.4) равен
, откуда модуль полного ускорения согласно (1.4) равен
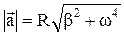 .
.
Дата добавления: 2015-09-18; просмотров: 697;
