Кинематика вращательного движения

При описании вращательного движения твердого тела относительно неподвижной в данной системе отсчета принято использовать векторные величины особого рода. В отличие от рассмотренных выше полярных векторов 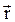(радиус-вектор), 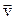(скорость), 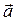(ускорение), направление которых естественным образом вытекает из природы самих величин, направление векторов, характеризующих вращательное движение, совпадает с осью вращения, поэтому их называют аксиальными(лат. axis – ось).

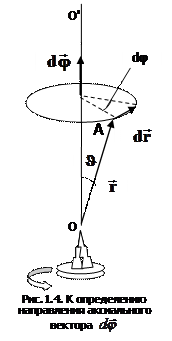Элементарный поворот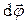– аксиальный вектор, модуль которого равен углу поворота dφ, а направление вдоль оси вращения ОО' (см. рис. 1.4) определяется правилом правого винта. Линейное перемещение 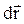произвольной точки А твердого тела связано с радиусом-вектором 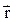и поворотом 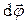соотношением 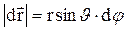или в векторном виде через векторное произведение:

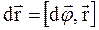. (1.9)

Соотношение (1.9) справедливо именно для бесконечно малого поворота .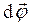

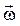Угловая скорость – аксиальный вектор, определяемый производной вектора поворота по времени

.

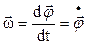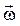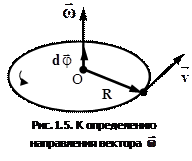
Вектор , как и вектор 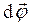, направлен вдоль оси вращения по правилу правого винта (рис.1.5).

Угловое ускорение 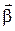– аксиальный вектор, определяемый производной вектора угловой скорости по времени

.

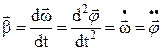При ускоренном движении вектор 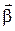по направлению совпадает с 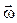(рис. 1.6,а), а при замедленном - векторы 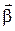и 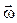направлены противоположно друг другу (рис. 1.6,б).

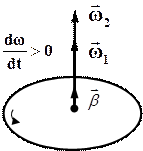
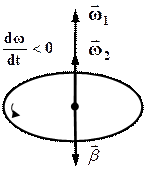
а) б)

Рис.1.6. Связь между направлениями векторов 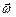и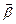

Важное замечание: решение всех задач на вращение твердого тела вокруг неподвижной оси по форме аналогично задачам на прямолинейное движение точки. Достаточно заменить линейные величины 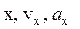на соответствующие им угловые 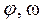и 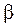, и мы получим уравнения, аналогичные (1.6)-(1.8).