Кинематические уравнения

Кинематические уравнения – это уравнения, показывающие зависимость основных кинематических характеристик (радиуса-вектора, координат, скорости, ускорения) от времени. В случае произвольного движения эти уравнения могут быть весьма сложными. Ниже приведены кинематические уравнения для некоторых простых случаев.

1.4.1. Равномерное прямолинейное движение

Это такое движение, при котором материальная точка (тело) за любые равные промежутки времени проходит одинаковые отрезки по прямой. Уравнение скорости для такого движения имеет вид:

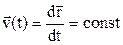. (1.5)

Выразим отсюда элементарное перемещение 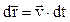и, проинтегрировав по времени в пределах (0, t), получим уравнение радиуса-вектора

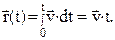
Полагая для простоты, что вектор скорости направлен вдоль оси ОХ, можно записать уравнение (1.5) в скалярной форме:

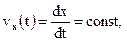(1.5,а)

откуда

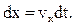(1.5.б)

Интегрируя выражение (1.5,б) по времени в пределах (0, t), получим уравнение пути:

.

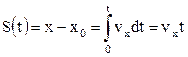Здесь х₀–начальная координата движущейся точки. Отсюда уравнение координаты имеет вид:

.

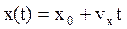Не следует забывать, что в зависимости от выбора положительного направления оси ОХ численное значение 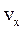может быть как положительным, так и отрицательным.

1.4.2. Равнопеременное движение

Это такое движение, при котором материальная точка (тело) за любые равные промежутки времени изменяет свою скорость на одну и ту же величину, т.е. имеет постоянное ускорение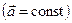. При равнопеременном прямолинейном движении возможны два варианта: равноускоренное и равнозамедленноедвижение.

Первый вариант соответствует ситуации, когда начальная скорость 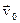либо равна 0, либо сонаправлена с ускорением 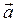. Примером такого варианта движения является падение тела с некоторой высоты: либо свободно отпущенного, либо брошенного с начальной скоростью вертикально вниз.

Второй вариант соответствует ситуации, когда 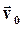направлена противоположно 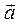. Например, движение тела, брошенного вертикально вверх (на участке траектории до верхней точки подъема).

Уравнение ускорения для прямолинейного вдоль оси ОХ равнопеременного движения в скалярной записи имеет вид:

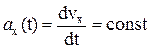. (1.6)

Элементарное изменение скорости выразится 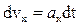, откуда интегрированием получаем приращение скорости за конечный промежуток времени (0, t)

,

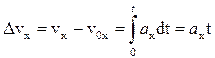и, окончательно, уравнение скорости:

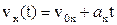. (1.7)

Далее, подставляя (1.7) в (1.5,б) и интегрируя с учетом начальных условий, получим уравнение координаты:

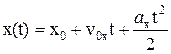. (1.8)