Вывод основного уравнения упругого режима

Считаем пласт упругим, горизонтальным и большой протяженности и в нём имеется одна скважина, тогда движение жидкости в пласте можно считать плоскорадиальным к точечному стоку (эксплуатационная скважина) или от точечного источника (нагнетательная скважина).

Рассмотрим процесс перераспределения давления при неустановившимся плоском радиальном движении жидкости. Для этого запишем уравнение пьезопроводности в цилиндрической системе координат

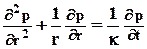. 5.12

Предположим, что возмущение вызвано мгновенным стоком, существовавшим в момент t=t^/ . Для этого случая решение уравнения (5.12) имеет вид

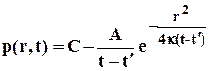, 5.13

где А и С- некоторые постоянные.

Найдём значения постоянных. Для этого будем считать, что в момент времени t=t^/ давление в пласте было р=р_к=const. Тогда при r>0 и при t=t^/ второй член правой части обращается в неопределённость типа ¥/¥ и определяется по правилу Лапиталя, что даёт С=р_к Таким образом,

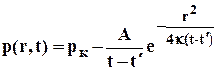, 5.14

Для определения коэффициента А воспользуемся соотношением (5.4) для определения объёма высвобождающейся жидкости для случая кольцевого элемента пласта с внутренним радиусом r, толщиной hи шириной dr, а также учтем падение давления Dр=p₀-p по (5.14)

dt_з=b^*Dрdt₀= 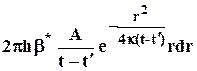. 5.15

После интегрирования (5.15) в пределах от 0 до ¥ получим объём жидкости t₂ , выделившейся из всего пласта и, следовательно, определим коэффициент А

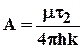. 5.16

Т.о. в случае скважины, введенной в неограниченный пласт в некоторый (начальный) момент времени и действующей мгновенно, изменение давления во времени определяется соотношением

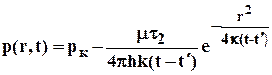, 5.17

Если скважина была введена в некоторый момент времени и действовала непрерывно с постоянным дебитом Q=Q₀ в течении времени dt^/, то за этот промежуток времени через сток выделяется из пласта объём dt₂=Qdt^/ и, следовательно, из (5.17) следует

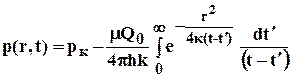, 5.18

Интеграл правой части носит название интегрально-показательной функции

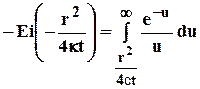
и с учетом данного обозначения решение для изменения давления запишется в виде

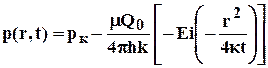, 5.19

Формула (5.19) является основной формулой теории упругого режима пласта.

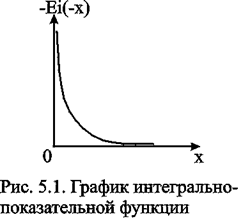
Интегрально-показательная функция имеет вид (рис.5.1) и обладает следующими свойствами:

* -Ei(-u) изменяется от 0 до ¥ при изменении аргумента от 0 до ¥;

* функция -Ei(-u) представляется в виде сходящегося ряда

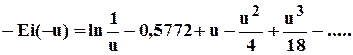5.20

Для малых значений u<1 можно принять

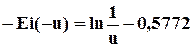5.21

Так погрешность применения (5.21) не превышает 0,25% при u<0,01; 5,7% - при u<0,1

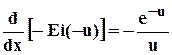. 5.22

С учетом соотношения (5.21) основное уравнение (5.19 перепишется в виде

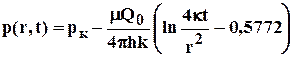, 5.23

Полученную зависимость можно использовать при числе Фурье 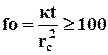с погрешностью не превышающей 0,6%. Практически это означает, чтоуже через 1 с после пуска скважины расчеты забойного давления, выполненные по формуле (5.23), будут иметь погрешность не превышающую 0,6%. Формулу (5.23) можно использовать и для расчета падения давления в конечном пласте, а именно, погрешность расчета давления при этом не превышает 1% , если r_к>1000r_c и fo<3,5^.10⁵ или Fo<0,35.

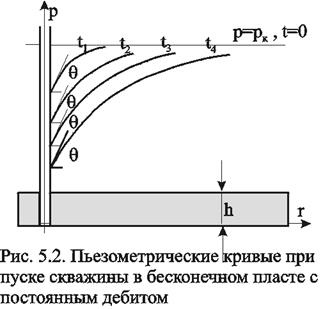
Рассмотрим пьезометрические кривые для бесконечного пласта, который эксплуатируется скважиной радиуса r_cc постоянным дебитом Q₀ (рис.5.2). Для точек вблизи забоя можно пользоваться формулой (5.23): дифференцируя её по координате r, найдём градиент давления

.

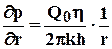Из этой формулы следует, что градиент давления для значений r, удовлетворяющих неравенству r²<<0,03^.4kt, практически не завист от времени и определяется по той же формуле, что для установившейся плоскорадиальной фильтрации несжимаемой жидкости. Для указанных значений rпьезометрические кривые представляют собой логарифмические линии (рис.5.2). Углы наклона касательных на забое скважины одинаковы для всех кривых.