Вращательное движение твердого тела вокруг неподвижной оси. Угловая скорость и угловое ускорение
Вращательным называется такое движение твердого тела, при котором хотя бы две точки тела, остаются неподвижными во время движения тела. Прямая, проведенная через эти точки, называется осью вращения. Точки тела, не лежащие на оси вращения, двигаются по окружностям, размещенным в плоскостях, перпендикулярных оси вращения, а центры окружностей находятся на этой оси.
Положение вращающегося тела (рис.10) определяется углом 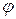 (углом поворота тела вокруг оси вращения), измеряемым в радианах. Угол
(углом поворота тела вокруг оси вращения), измеряемым в радианах. Угол 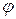 считается положительным, если из положительного направления оси вращения он виден отложенным против хода часовой стрелки.
считается положительным, если из положительного направления оси вращения он виден отложенным против хода часовой стрелки.
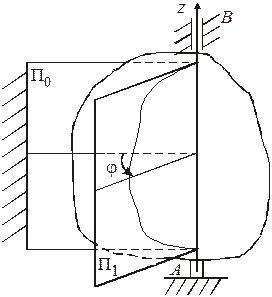
Рисунок 10
Зависимость угла поворота от времени
 (109)
(109)
является уравнением вращательного движения тела вокруг неподвижной оси.
Кинематическими характеристиками вращательного движения тела является угловая скорость 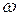 (омега) и угловое ускорение
(омега) и угловое ускорение 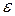 (эпсилон).
(эпсилон).
Угловой скоростью называется физическая величина, которая характеризует изменения угла поворота 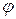 со временем.
со временем.
Угловая скорость тела при его вращении вокруг неподвижной оси равняется первой производной по времени от угла поворота:
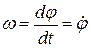 . (110)
. (110)
Если 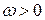 , то тело в данный момент времени вращается в положительном направлении, то есть против часовой стрелки.
, то тело в данный момент времени вращается в положительном направлении, то есть против часовой стрелки.
Единица измерения угловой скорости 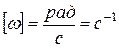 .
.
Иногда угловую скорость в технике выражают величиной n оборотов в минуту ( 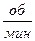 ). Тогда угловая скорость
). Тогда угловая скорость 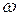 в радианах за секунду вычисляется по формуле
в радианах за секунду вычисляется по формуле
 . (111)
. (111)
Угловым ускорением называется физическая величина, которая характеризует быстроту изменения со временем угловой скорости тела.
Угловое ускорение тела равняется первой производной по времени от угловой скорости или второй производной от угла поворота тела
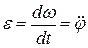 . (112)
. (112)
Единица измерения углового ускорения – 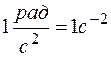 .
.
При ускоренном вращении, если модуль угловой скорости со временем увеличивается, угловая скорость и угловое ускорение имеют одинаковые знаки. В случае замедленного вращения знак углового ускорения противоположен знаку угловой скорости.
В частных случаях различают равномерное и равнопеременное вращательные движения тела.
При равномерном вращении, когда угловая скорость тела не изменяется, то есть 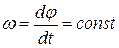 , уравнение равномерного вращения имеет вид:
, уравнение равномерного вращения имеет вид:
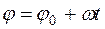 . (113)
. (113)
где 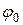 – начальный угол поворота.
– начальный угол поворота.
Если угловое ускорение тела во время движения остается постоянным, то есть 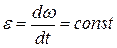 , то вращения называют равнопеременным.
, то вращения называют равнопеременным.
При равнопеременном вращении угловая скорость тела изменяется по закону
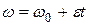 , (114)
, (114)
а уравнение равнопеременного вращения имеет вид
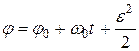 . (115)
. (115)
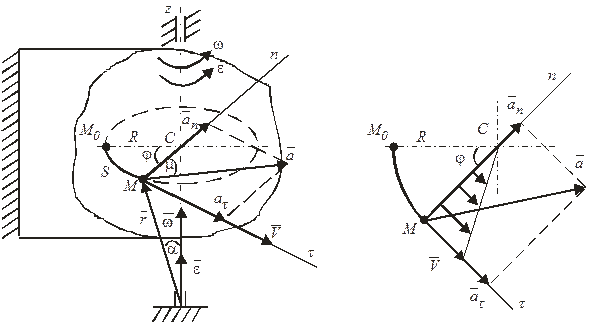
Кинематические характеристики любой точки вращающегося тела (рис. 11) определяются с помощью следующих формул:
- путь, пройденный точкой по окружности 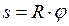 ;
;
- линейная скорость точки 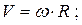 ;
;
- касательное ускорение точки 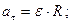
- нормальное ускорение точки 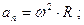
- полное ускорение точки 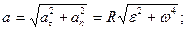
- угол между направлениями полного и нормального ускорений  . (116)
. (116)
а) б)
Рисунок 11
При передаче вращательного движения от тела 1 к телу 2 (рис 12) выполняются такие соотношения:
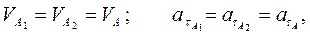
или  и
и 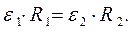
Отсюда получим передаточное отношение механизма:
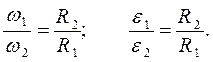

Рисунок 12
Для передаточных механизмов с зубчатыми колесами можно записать:
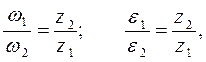
где  - количество зубцов соответственно первого и второго колес.
- количество зубцов соответственно первого и второго колес.
Дата добавления: 2015-09-14; просмотров: 2089;
