Методика и примеры решения задач. Решение задач кинематики простейших движений твердого тела осуществляют с применением вышеприведенных формул.
Решение задач кинематики простейших движений твердого тела осуществляют с применением вышеприведенных формул.
Пример 4
Механизм лебедки, показанный на рис. 13, перемещает груз 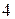 благодаря вращению шкива
благодаря вращению шкива 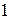 радиусом, который с помощью передачи паса связан с шкивом, радиус которого
радиусом, который с помощью передачи паса связан с шкивом, радиус которого 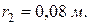 С этим шкивом жестко связана шестерня, которая сцеплена с шестерней, насаженной на вал барабана радиусом .
С этим шкивом жестко связана шестерня, которая сцеплена с шестерней, насаженной на вал барабана радиусом . 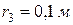 Определить в момент времени
Определить в момент времени 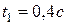 скорость и ускорение точки
скорость и ускорение точки 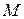 барабана, а также высоту подъема груза за это время, если шкив
барабана, а также высоту подъема груза за это время, если шкив 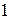 вращается за законом, а количество зубцов шестерен
вращается за законом, а количество зубцов шестерен 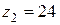 и .
и .
Решение
Найдем угловую скорость и угловое ускорение шкива 1.
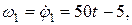
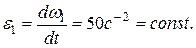
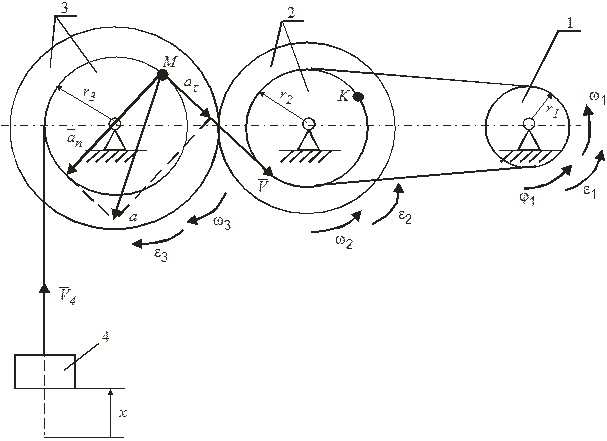
Рисунок 13
Поскольку ремень, который соединяет шкивы 1 и 2 нерастяжимый, то скорость точки 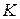 шкива 2 равняется скорости точки, которая лежит на ободе шкива, то есть, откуда определим угловую скорость колеса
шкива 2 равняется скорости точки, которая лежит на ободе шкива, то есть, откуда определим угловую скорость колеса 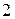 :
:
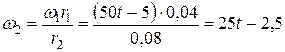 .
.
Угловое ускорение колеса 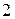
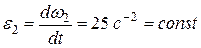 .
.
Скорость точки касания зубчатых колес 2 и 3
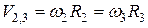 ,
,
откуда
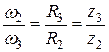 .
.
Следовательно, угловые скорости вращения обратно пропорциональны радиусам или количеству зубцов:
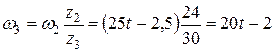 .
.
Аналогичная зависимость между угловыми ускорениями: 
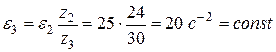 .
.
В момент времени 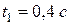 имеем
имеем 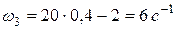 .
.
Определим модули скорости, касательного, нормального 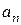 и полного
и полного 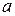 ускорения точки
ускорения точки 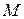 .
.
В момент времени, 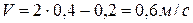 имеем:
имеем:
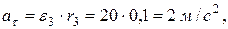
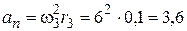 м/с2
м/с2 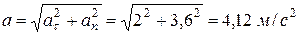 .
.
Так как скорость груза равняется скорости точки 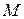
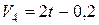 , то закон поступательного движения найдем, интегрируя выражение скорости
, то закон поступательного движения найдем, интегрируя выражение скорости
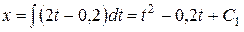 .
.
Приняв начало отсчета оси х в начальном положении груза, когда, получим 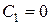 , и за время
, и за время 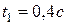 груз поднимется на высоту
груз поднимется на высоту
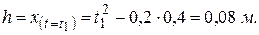
Пример 5
Ускорение точки 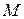 диска, который вращается вокруг неподвижной оси
диска, который вращается вокруг неподвижной оси 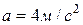 (рис. 14). Определить угловую скорость этого диска и скорость точки, если радиус диска, а угол наклона полного ускорения точки
(рис. 14). Определить угловую скорость этого диска и скорость точки, если радиус диска, а угол наклона полного ускорения точки 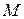 к нормали
к нормали 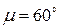 .
.
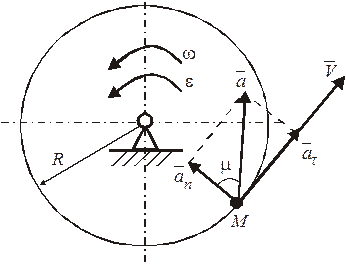
Рисунок 14
Решение
Поскольку угол между вектором полного ускорения точки 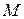 и вектором ее нормального ускорения известен, то ускорение
и вектором ее нормального ускорения известен, то ускорение
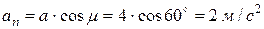 .
.
Нормальное ускорение точки при вращательном движении связано с угловой скоростью тела зависимостью 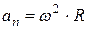 . Откуда
. Откуда
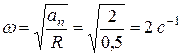 .
.
Скорость точки 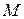 :
:
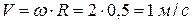 .
.
Дата добавления: 2015-09-14; просмотров: 1617;
