Методика и примеры решения задач. Для решения задач кинематики нужно знать закон движения точки,, который или задают явно в условии задачи
Для решения задач кинематики нужно знать закон движения точки,, который или задают явно в условии задачи, или можно определить из известного движения механизма, одному из звеньев которого принадлежит рассматриваемая точка.
Кинематические характеристики движения точки (скорость, ускорение, касательное и нормальное ускорение и др.) определяются по вышеприведенным для каждого из способов задания формулам.
При задании движения точки координатным способом её касательное и нормальное ускорения находят после вычисления скорости 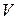 и ускорения a. При этом, взяв производную по времени от найденного выражения скорости
и ускорения a. При этом, взяв производную по времени от найденного выражения скорости 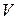 , определяют касательное ускорение
, определяют касательное ускорение 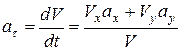 . Нормальное ускорение
. Нормальное ускорение 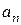 находят из зависимости
находят из зависимости 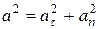 . Радиус кривизны траектории
. Радиус кривизны траектории 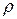 определяют из формулы
определяют из формулы 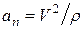 .
.
Если движение задано естественным способом, а уравнение движения точки по траектории не задано, но известен характер движения точки, то для составления уравнения движения применяют формулы кинематических зависимостей, приведенные в таблице 1.
Пример 1
Найти траекторию точки  шатуна
шатуна 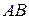 механизма (рис. 5) кривошипного шатуна, если длина кривошипа, длина шатуна, расстояние, угол наклона кривошипа к горизонтали изменяется по закону
механизма (рис. 5) кривошипного шатуна, если длина кривошипа, длина шатуна, расстояние, угол наклона кривошипа к горизонтали изменяется по закону 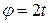 советов. Найти также скорость, ускорение и радиус кривизны траектории точки в момент времени
советов. Найти также скорость, ускорение и радиус кривизны траектории точки в момент времени 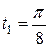 сек.
сек.
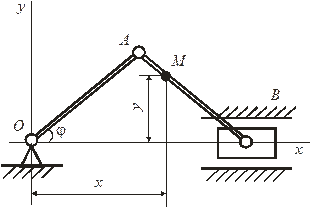
Рисунок 5
Решение
В данной задаче закон движения точки непосредственно не задан, потому в первую очередь установим уравнение движения точки 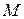 в координатной форме.
в координатной форме.
Для этого проведем оси координат х и у, поместив их начало в точке 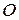 и определим координаты точки
и определим координаты точки 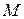 как функции угла
как функции угла 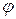 . Из рисунка 5 видно, что
. Из рисунка 5 видно, что
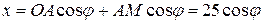 ;
;
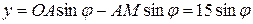 .
.
Или с учетом зависимости угла 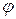 от времени:
от времени:
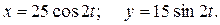
Для определения уравнения траектории точки 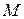 исключим время
исключим время 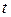 из уравнения движения
из уравнения движения
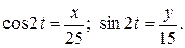
Применив известную зависимость 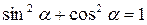 , возведем обе части этих равенств в квадрат и сложим их:
, возведем обе части этих равенств в квадрат и сложим их:
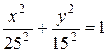 .
.
Следовательно, траекторией точки 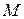 будет эллипс с центром в точке О, полуоси которого равны 25 см и 15 см. Построим траекторию в выбранном масштабе и покажем на ней положение точки
будет эллипс с центром в точке О, полуоси которого равны 25 см и 15 см. Построим траекторию в выбранном масштабе и покажем на ней положение точки 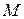 в заданный момент времени, когда ее координаты будут
в заданный момент времени, когда ее координаты будут
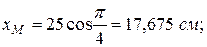
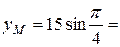
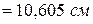 (рис. 6).
(рис. 6).
Проекции вектора скорости на оси координат
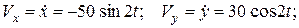
и модуль скорости в любой момент времени:
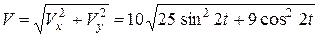 .
.
Направление вектора 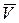 в любой момент времени определяется направляющими косинусами:
в любой момент времени определяется направляющими косинусами:
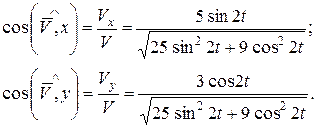
Ускорение точки 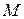 найдем через его проекции на оси координат согласно с формулами (93) и (94):
найдем через его проекции на оси координат согласно с формулами (93) и (94):
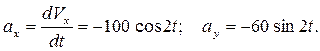
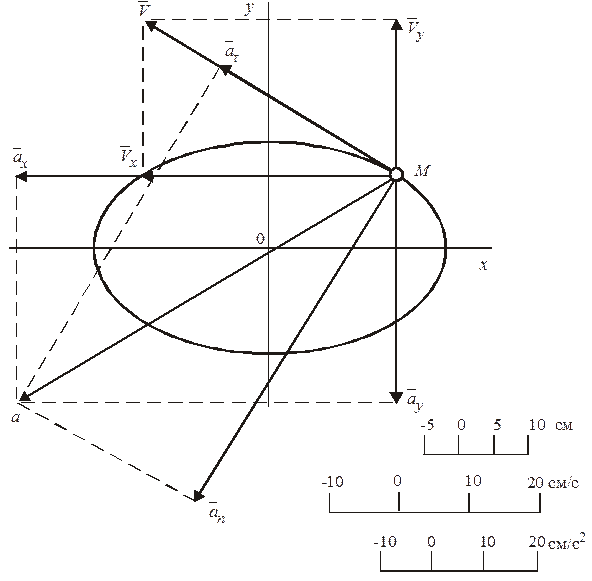
Рисунок 6
Модуль вектора ускорения
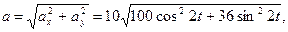
а направляющие конусы вектора ускорения:
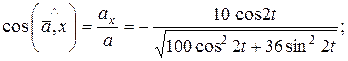
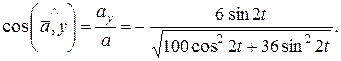
Определим найденные величины в момент времени 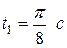 :
:
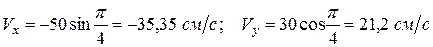 ;
;
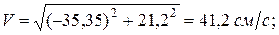
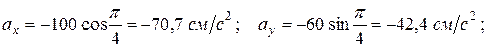
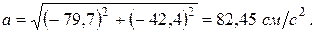
Касательное ускорение найдем, дифференцируя величину скорости точки:
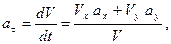
и в момент времени 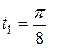 имеем:
имеем:
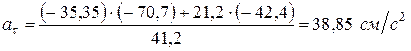 .
.
Найдем нормальное ускорение точки по формуле
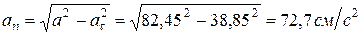 .
.
Радиус кривизны траектории в данной точке М1 в соответствии с формулой (105) равняется
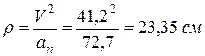 .
.
В заданном положении точки в масштабе строим вектор 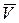 с составляющими
с составляющими 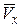 и
и 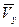 , направляя вектор скорости по касательной к траектории (см. рис. 6). Вектор
, направляя вектор скорости по касательной к траектории (см. рис. 6). Вектор 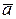 находим через составляющие
находим через составляющие 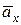 и
и 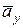 , а также через составляющие
, а также через составляющие 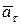 и
и 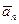 , как показано на рис. 6. Выполнение условий построения этих векторов подтверждает правильность проведенных вычислений.
, как показано на рис. 6. Выполнение условий построения этих векторов подтверждает правильность проведенных вычислений.
Пример 2
Точка двигается по окружности радиуса 25 м по закону 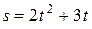 (
( 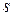 – в метрах,
– в метрах, 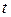 – в секундах). Определить ускорение точки в тот момент времени, когда ее дуговая координата будет равняться 27 м.
– в секундах). Определить ускорение точки в тот момент времени, когда ее дуговая координата будет равняться 27 м.
Решение
Движение точки задано естественным способом. Выберем на траектории начальное положение 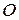 , положительное направление движения (рис. 7) и покажем положение
, положительное направление движения (рис. 7) и покажем положение 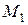 точки в тот момент времени, когда ее дуговая координата соответствует центральному углу
точки в тот момент времени, когда ее дуговая координата соответствует центральному углу 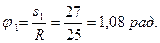 . Найдем время
. Найдем время 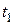 движения точки, подставив в уравнение движения значение
движения точки, подставив в уравнение движения значение 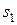 и
и 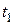 :
: 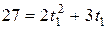 . Из квадратного уравнения, найдем:
. Из квадратного уравнения, найдем:
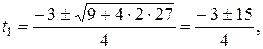
то есть 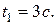
Величина скорости и ускорения точки равняются:
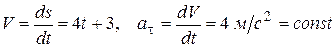 .
.
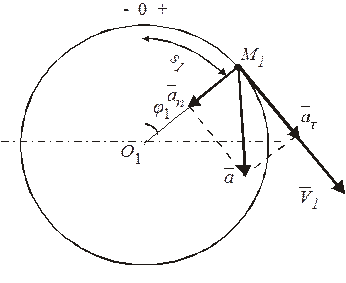
Рисунок 7
При времени 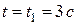 скорость
скорость 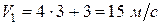 . Тогда нормальное ускорение точки в этот момент времени
. Тогда нормальное ускорение точки в этот момент времени
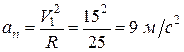 ,
,
а полное ускорение точки в положении 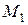
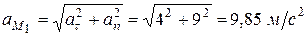 .
.
Пример 3
Отходя от станции, поезд движется равноускоренно по дуге окружности радиусом 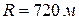 . Пройдя путь
. Пройдя путь 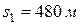 , поезд получил скорость
, поезд получил скорость 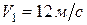 . Найти время, за какой поезд прошел это расстояние, и его полное ускорение в это время.
. Найти время, за какой поезд прошел это расстояние, и его полное ускорение в это время.
Решение
Рассматриваем поезд как подвижную точку, траектория которой известна. Для нахождения искомых величин воспользуемся естественным способом задания движения, выбрав начало отсчета на траектории в начальном положении поезда, когда при 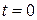 имеем
имеем 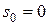 и
и 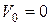 . Тогда равнопеременное движение поезда опишется зависимостями:
. Тогда равнопеременное движение поезда опишется зависимостями:
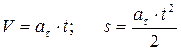 .
.
Решая совместно эти уравнения, находим 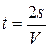 и
и 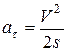 , откуда искомое время движения и касательное ускорение будут
, откуда искомое время движения и касательное ускорение будут
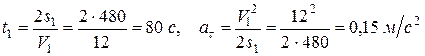 .
.
Полное ускорение определим по формуле (106)
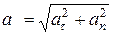 ,
,
где 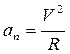 , или при числовых значениях задачи
, или при числовых значениях задачи
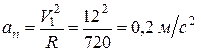 .
.
Окончательно
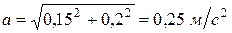 .
.
Вопросы для самоконтроля
1 Что изучает кинематика? Сформулируйте основную задачу кинематики точки.
2 Дайте определение системы отсчета, закона движения точки.
3 Что такое траектория точки, какой она может быть?
4 Назовите существующие способы задания движения точки. В чем заключается каждый из этих способов?
5 Как при координатном способе задания движения точки определяется ее траектория?
6 При каких условиях пройденный точкой путь и дуговая координата точки на траектории совпадают?
7 Запишите формулу для определения вектора скорости точки. Как направлен вектор скорости точки?
8 Запишите формулы для определения проекций скорости точки на декартовы оси координат.
9 Как по известным проекциям 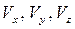 скорости точки найти ее модуль и направление?
скорости точки найти ее модуль и направление?
10 Запишите формулу для определения вектора ускорения точки и укажите направление этого вектора в пространстве. В какой плоскости лежит вектор ускорения точки?
11 Как определяется алгебраическая скорость точки по известному естественному уравнению движения точки? Приведите формулу для ее определения и укажите ее направление.
12 Как определяется ускорение точки при координатном способе задания движения?
13 Охарактеризуйте естественные оси координат? Как они направлены?
14 В какой плоскости размещается вектор ускорения по отношению к осям естественного трехгранника, куда он направлен?
15 Чему равняются проекции ускорения точки на касательную ось и главную нормаль к траектории?
16 В каких случаях касательное ускорение точки равняется нулю? Нормальное ускорение точки равняется нулю?
17 Какое движение точки называется равномерным, равнопеременным?
Дата добавления: 2015-09-14; просмотров: 2645;
