Определение скоростей точек плоской фигуры
Для определения скорости любой точки плоской фигуры применяют следующие методы.
1) С помощью теоремы о скоростях точек плоской фигуры (рис. 17).
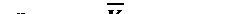
Рисунок 17
Скорость любой точки плоской фигуры равняется геометрической сумме скорости полюса и скорости этой точки во вращательном движении плоской фигуры вокруг полюса, т.е.
.
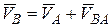В этом выражении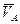 
– скорость полюса 
,
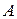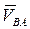- скорость точки 
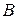при вращении плоской фигуры вокруг полюса .
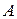При этом скорость 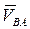направлена перпендикулярно к отрезку 
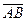и вычисляется по формуле 
.
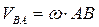Модуль и направление скорости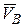 
определяются построением соответствующего параллелограмма (см. рис. 17).
2) С помощью теоремы о проекциях скоростей (рис. 18).
Рисунок 18
Проекции скоростей двух точек твердого тела на прямую, которая проходит через эти точки, уровни между собой , т.е..
,
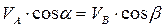Где α и β – углы наклона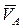 
и 
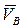к линии АB соответственно.
Эта теорема позволяет легко находит скорость данной точки тела, если известные направление скорости этой точки та скорость любой другой точки этого тела.
3) С помощью мгновенного центра скоростей.
Плоское движение в данный момент времени можно рассматривать как вращательное движение вокруг мгновенного центра вращения или мгновенного центра скоростей.
Мгновенным центром скоростей (м.ц.с.) называют связанную с плоской фигурой точку, скорость которой в данный момент времени равняется нулю.
Мгновенный центр скоростей (точка Р) находится (рис. 19) на линии, проведенной через некоторую точку А плоской фигуры перпендикулярно вектору 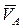скорости этой точки так, что угол 90° отложен в направлении угловой скорости ω плоской фигуры.При этом расстояние от точки
плоской фигуры до мгновенного центра скоростей равно частному от деления модуля скорости этой точки на угловую скорость, т.е.:
.
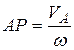Рисунок 19
Исходя из этого, можно сделать вывод: угловая скорость плоской фигуры в данный момент времени равняется отношению скорости одной из ее точек к длине отрезка, который соединяет точку из м.ц.с., а скорости точек тела пропорциональны расстояниям от этих точек к м.ц.с.
Таким образом, зная величину скорости одной из точек плоской фигуры и положение её мгновенного центра скоростей, по зависимости
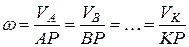
можно определить (рис.20) скорость любой точки и угловую скорость плоской фигуры.
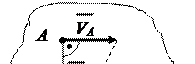
Рисунок 20
Существует несколько типичных приемов нахождения положения мгновенного центра скоростей.
1) Если известны скорость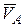 
одной из точек плоской фигуры и ее угловая скорость 
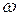, то м.ц.с. находится на перпендикуляре к вектору 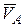скорости точки, отложенному в направлении вращения плоской фигуры на расстоянии 
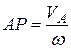(см. рис.19).
2) Если известны направления скоростей двух точек плоской фигуры и векторы этих точек непараллельные между собой (рис. 21), то м.ц.с. находится на пересечении перпендикуляров к векторам скоростей этих точек.
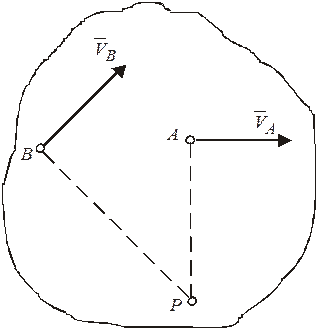
Рисунок 21
3) Если скорости двух точек плоской фигуры параллельны между собой и перпендикулярны к отрезку, который соединяет эти точки, а модули этих скоростей известны и разные, то м.ц.с. лежит на пересечении общего перпендикуляра к векторам скоростей этих точек и линии, проведенной через концы этих векторов (рис.22).
а) б)
Рисунок 22
4) Если скорости двух точек параллельны между собой, а линия размещения этих точек не перпендикулярна к их скоростям (рис. 23), то м.ц.с. находится в бесконечности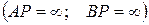 
, а угловая скорость плоской фигуры 
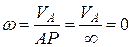. В этом случае тело осуществляет мгновенно поступательное движение, при котором скорости всех точек в данный момент времени уровни за величиной и одинаково направленные.
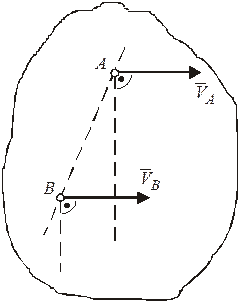
Рисунок 23
5) Если плоское движение осуществляется путем качения без скольжения одного тела неподвижной поверхностью другого (рис.24), то м.ц.с. находится в точке контакта тела с неподвижной поверхностью, так как при отсутствии скольжения скорость этой точки подвижного тела равняется нулю.
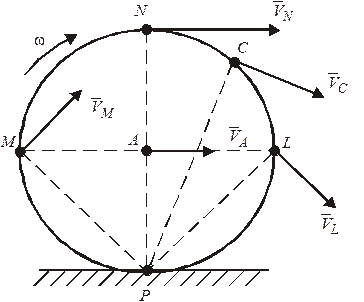
Рисунок 24
Дата добавления: 2015-09-14; просмотров: 888;