Методика и примеры решения задач
Задачи, для решения которых используют формулы кинематики плоского движения тела, касаются преимущественно определения скоростей и ускорений точек разных механизмов и определения угловых скоростей и ускорений звеньев этих механизмов за заданным движением ведущего звена механизма.
Механизм, движение которого рассматривается, нужно изображать на рисунку в том положении, для которого нужно определить соответствующие характеристики.
При определении угловых скоростей и скоростей точек нужно знать модуль и направление скорости какой-либо одной из точек и направление скорости другой точки этого тела, что позволяет найти положение мгновенного центра скоростей (кроме случая 5, рассмотренного в разделе 3.1.2). При этом нужно понимать, что каждое звено механизма, которое осуществляет плоскопараллельное движение, имеет в данный момент времени свой мгновенный центр скоростей и свою угловую скорость.
Для определения углового ускорения плоской фигуры и ускорений ее точек применяют векторное выражение (132), учитывая, что при криволинейном движении точек их ускорения имеют касательные и нормальные составляющие. Поставленная цель является досягаемой, если известны векторы скорости и ускорения одной из точек этой фигуры, а также траектория другой точки фигуры или положения мгновенного центра скоростей.
Это позволяет найти модули и направления большинства из ускорений выражения (132), оставив неизвестными только две величины (модули, направления). Потом, проектируя векторное уравнение (132) на выбранные оси координат, получают два алгебраических уравнения, за которым вычисляют неизвестные величины.
Угловое ускорение 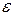 плоской фигуры чаще всего находят после вычисления касательного ускорения одной из точек фигуры во вращательном движении вокруг полюса, применяя зависимость (133). Но в случае качения без скольжения колеса неподвижной поверхностью (див.рис.93), когда расстояние
плоской фигуры чаще всего находят после вычисления касательного ускорения одной из точек фигуры во вращательном движении вокруг полюса, применяя зависимость (133). Но в случае качения без скольжения колеса неподвижной поверхностью (див.рис.93), когда расстояние 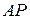 центра колеса к м.ц.с. остается неизменной, угловое ускорение находят путем дифференцирования по времени выражения угловой скорости
центра колеса к м.ц.с. остается неизменной, угловое ускорение находят путем дифференцирования по времени выражения угловой скорости 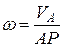 :
:
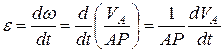 ,
,
или
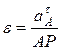 .
.
Пример 6
В плоском механизме, изображенном на рис 95, длина звеньев которого l1=OA=0,6м, l2=AB=1,8м, l3=O1B=2,4м, О1D=0,8м и l4=DE=1,2м, кривошип 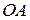 вращается с угловым ускорением
вращается с угловым ускорением 
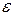 1=10с-2. Определить скорости VB, VE точек
1=10с-2. Определить скорости VB, VE точек  механизма и угловые скорости
механизма и угловые скорости  w2, w4 стержней
w2, w4 стержней 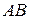 и
и 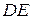 , а также ускорение
, а также ускорение 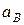 точки
точки 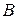 и угловое ускорение
и угловое ускорение 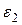 стержня
стержня 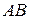 в положении механизма, когда углы
в положении механизма, когда углы 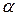 =60
=60 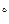 ,
, 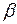 =90
=90 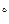 ,
, 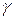 =45
=45 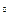 ,
, 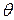 =120
=120 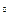 , а угловая скорость кривошипа ОА
, а угловая скорость кривошипа ОА 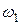 =6с
=6с 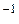 , его угловое ускорение ε1=10с-2.
, его угловое ускорение ε1=10с-2.
Решение
Строим положение механизма в соответствии с заданными углами (рис.96). Определяем скорость точек. Скорость 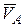 точки А перпендикулярна к кривошипу
точки А перпендикулярна к кривошипу 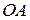 . Ее модуль
. Ее модуль 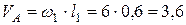 м/c.
м/c.
Скорость 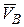 точки В, которая одновременно принадлежит шатуну АВ и кривошипу О1В, перпендикулярна к кривошипу О1В. Мгновенный центр скоростей Р2 стержня АВ находится в точке пересечения перпендикуляров, проведенных из точек А и В к их скоростям. Скорости точек стержня АВ (звена 2) и его угловая скорость связаны зависимостью
точки В, которая одновременно принадлежит шатуну АВ и кривошипу О1В, перпендикулярна к кривошипу О1В. Мгновенный центр скоростей Р2 стержня АВ находится в точке пересечения перпендикуляров, проведенных из точек А и В к их скоростям. Скорости точек стержня АВ (звена 2) и его угловая скорость связаны зависимостью
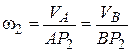 .
.
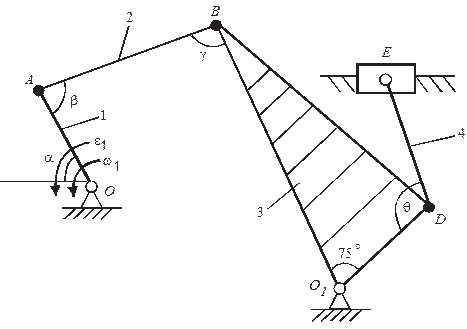
Рисунок 95
|
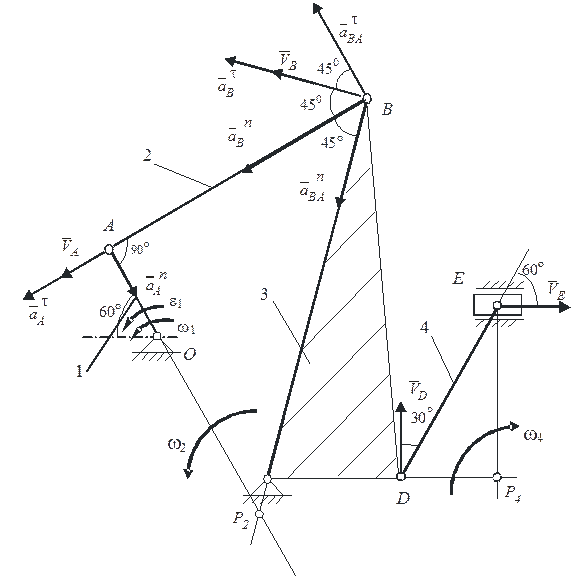
Рисунок 96
Как видно из рисунка 96, треугольник АBP2 прямоугольный и равнобедренный, поэтому: АР2=АВ=l2=1,8м. Исходя из этого, получим:
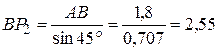 м.
м.
Итак
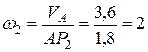 с-1;
с-1; 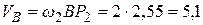 м.
м.
Для определения скорости точки  , которая принадлежит стержню
, которая принадлежит стержню  , нужно сначала найти скорость точки
, нужно сначала найти скорость точки 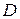 . Так как точка
. Так как точка 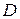 вместе с точкой
вместе с точкой 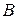 принадлежит звену 3, которое вращается около неподвижной точки
принадлежит звену 3, которое вращается около неподвижной точки 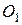 с угловой скоростью
с угловой скоростью 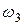 , то скорость точки
, то скорость точки 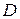 найдем из пропорции:
найдем из пропорции:
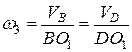 ,
, 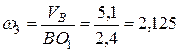 с-1,
с-1,
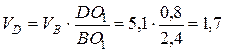 м/c.
м/c.
Вектор 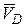 направлен перпендикулярно к стержню
направлен перпендикулярно к стержню 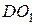 так, чтоб угловая скорость
так, чтоб угловая скорость 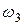 была направлена против хода часовой стрелки относительно направления
была направлена против хода часовой стрелки относительно направления 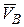 .
.
Направление вектора 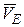 определим, исходя из того, что точка
определим, исходя из того, что точка 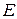 принадлежит одновременно ползуну, который движется вдоль направляющих поступательно. Теперь, зная
принадлежит одновременно ползуну, который движется вдоль направляющих поступательно. Теперь, зная 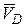 и направление
и направление 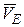 , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня
, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня 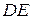 ) на прямую, которая объединяет эти точки. Сначала по этой теореме установим, в какую сторону направлен вектор
) на прямую, которая объединяет эти точки. Сначала по этой теореме установим, в какую сторону направлен вектор 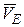 (проекции скоростей должны иметь одинаковые знаки). Потом, вычисляя эти проекции, находим:
(проекции скоростей должны иметь одинаковые знаки). Потом, вычисляя эти проекции, находим:
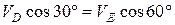 ,
,
Откуда
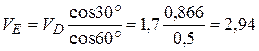 м.
м.
Для определения угловой скорости стержня 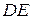 (звена 4) найдем положение мгновенного центра скоростей
(звена 4) найдем положение мгновенного центра скоростей 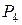 в точке пересечения перпендикуляров, проведенных из точек
в точке пересечения перпендикуляров, проведенных из точек 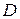 и
и 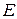 к их скоростям. Тогда:
к их скоростям. Тогда:
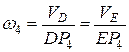 .
.
Из прямоугольного треугольника 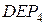 найдем:
найдем:
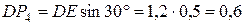 м.
м.
Итак
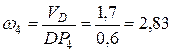 с-1.
с-1.
Определяем ускорения точек. Ускорение точки 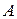 состоит из касательного и нормального ускорений:
состоит из касательного и нормального ускорений:
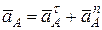 ,
,
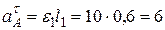 м/с2,
м/с2,
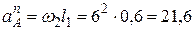 м/с2.
м/с2.
Вектор 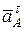 направленный перпендикулярно к
направленный перпендикулярно к 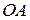 , а вектор
, а вектор 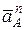 направленный от точки
направленный от точки 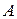 к точке
к точке 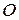 .
.
Для определения ускорения точки 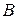 воспользуемся уравнением
воспользуемся уравнением

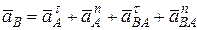 .
.
Так как точка 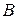 принадлежит не только стержню
принадлежит не только стержню 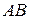 , но и стержню
, но и стержню 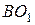 (звену 4), который вращается около неподвижной точки
(звену 4), который вращается около неподвижной точки 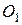 , то ускорение точки В тоже состоит из касательного и нормального ускорений, то есть
, то ускорение точки В тоже состоит из касательного и нормального ускорений, то есть
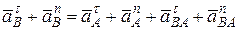 .
.
Вектор 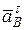 направляем перпендикулярно к стержню
направляем перпендикулярно к стержню 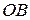 в ту или другую сторону. Его вычисление по формуле
в ту или другую сторону. Его вычисление по формуле 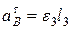 невозможно, так как значение
невозможно, так как значение 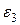 неизвестно. Нормальное ускорение точки
неизвестно. Нормальное ускорение точки 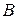
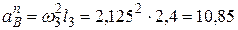 м/с2
м/с2
и вектор 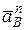 направляем от точки
направляем от точки 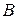 к точке
к точке 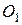 .
.
Вектор 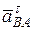 направляем перпендикулярно к стержню
направляем перпендикулярно к стержню 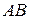 в любую сторону, а вектор
в любую сторону, а вектор 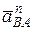 – вдоль
– вдоль 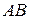 от точки
от точки 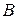 к точке
к точке 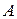 , и находим числовое значение:
, и находим числовое значение:
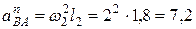 м/с2.
м/с2.
Таким образом, в величинах, которые входят в векторное уравнение, неизвестны только числовые значения 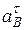 і
і 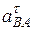 . Чтоб найти эти величины, спроецируем обе части векторного уравнения на две произвольно выбранные перпендикулярные оси
. Чтоб найти эти величины, спроецируем обе части векторного уравнения на две произвольно выбранные перпендикулярные оси 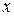 и
и 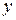 . Направляем одну из осей (ось
. Направляем одну из осей (ось 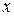 ) вдоль стержня
) вдоль стержня 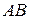 и в результате проектирования получим:
и в результате проектирования получим:
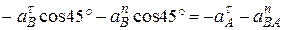 ,
,
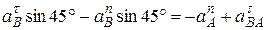 .
.
Из этих алгебраических уравнений находим:
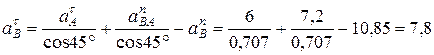 м/с2;
м/с2;
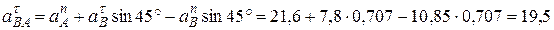 м/с2.
м/с2.
Тогда ускорение точки 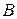 :
:
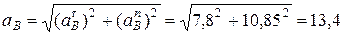 м/с2.
м/с2.
Угловое ускорение стержня 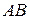 :
:
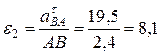 с-2.
с-2.
Ответ:
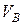 =5,1 м/с;
=5,1 м/с; 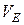 =2,85 м/с;
=2,85 м/с; 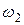 =2с-1;
=2с-1; 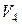 =2,83 с
=2,83 с 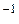 ;
; 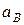 =13,4 м/с;
=13,4 м/с; 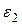 =8,1 с-2.
=8,1 с-2.
Пример 7
Шестерня 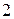 радиуса
радиуса 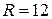 см планетарного механизма (рис. 97,а) приводится в движение кривошипом
см планетарного механизма (рис. 97,а) приводится в движение кривошипом 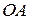 , который вращается вокруг оси
, который вращается вокруг оси 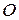 неподвижной шестерни 1 с тем же радиусом. Кривошип
неподвижной шестерни 1 с тем же радиусом. Кривошип 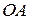 вращается с угловым ускорением ε0=8с-2, имея в данный момент угловую скорость
вращается с угловым ускорением ε0=8с-2, имея в данный момент угловую скорость 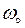 =2с-1. Определить скорость и ускорение точки
=2с-1. Определить скорость и ускорение точки 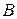 подвижной шестерни механизма, если
подвижной шестерни механизма, если 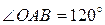 .
.
Решение
В данном механизме кривошип 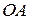 совершает вращательное движение, а шестерня 2 движется плоскопараллельно. Кинематические характеристики точки
совершает вращательное движение, а шестерня 2 движется плоскопараллельно. Кинематические характеристики точки 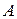 вычислим, рассматривая вращательное движение кривошипа
вычислим, рассматривая вращательное движение кривошипа 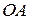 (рис. 97,б):
(рис. 97,б):
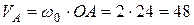 см/с;
см/с;
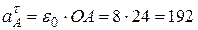 см/с2;
см/с2;
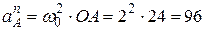 см/с2.
см/с2.
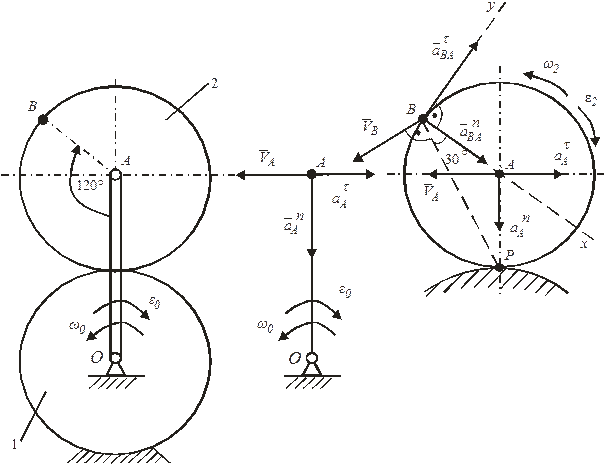
а) б) в)
Рисунок 97
Направления векторов  ,
,  ,
,  показаны на рис. 97,б.
показаны на рис. 97,б.
Теперь рассмотрим плоское движение шестерни 2, для которой мгновенный центр скоростей 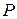 находится в точке ее контакта с неподвижной шестерней 1, а расстояние
находится в точке ее контакта с неподвижной шестерней 1, а расстояние 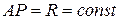 .
.
Тогда
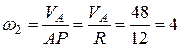 с-2,
с-2, 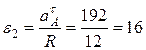 с-2,
с-2,
а 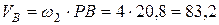 см/с, где расстояние
см/с, где расстояние 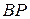 найдено из равнобедренного треугольника
найдено из равнобедренного треугольника 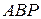 :
:
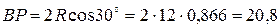 см.
см.
Направляем вектор 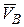 перпендикулярно к
перпендикулярно к 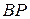 , как показано на рис. 97, в.
, как показано на рис. 97, в.
Ускорение точки 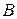 найдем по формуле распределения ускорений относительно полюса
найдем по формуле распределения ускорений относительно полюса 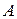 :
:
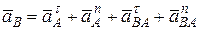 .
.
Составляющие ускорения точки 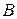 во вращательном движении вокруг полюса
во вращательном движении вокруг полюса 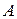 найдем по формулам:
найдем по формулам:
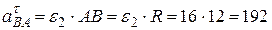 см/с2;
см/с2;
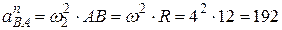 см/с2.
см/с2.
Направления составляющих вектора ускорения точки 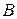 показаны на рис. 97, в. Выбрав оси координат (див. рис. 97, в), определим проекции вектора
показаны на рис. 97, в. Выбрав оси координат (див. рис. 97, в), определим проекции вектора 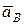 на эти оси:
на эти оси:
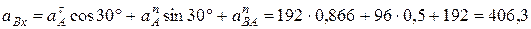 см/с2,
см/с2,
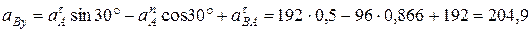 см/с2.
см/с2.
тогда
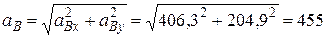 см/с2.
см/с2.
Вопросы для самоконтроля
1 Какое движение тела называют плоскопараллельным или плоским?
2 Какими уравнениями задают плоское движение тела?
3 Как связаны между собой скорость произвольной точки плоской фигуры и скорость точки, выбранной как полюс?
4 Сформулируйте теорему о проекциях скоростей двух точек.
5 Что называется мгновенным центром скоростей?
6 Как определяется положение мгновенного центра скоростей?
7 Где находится мгновенный центр скоростей плоской фигуры, которая совершает мгновенно поступательное движение?
8 Как распределяются скорости точек плоской фигуры относительно ее мгновенного центра скоростей?
9 Как определяется ускорение произвольной точки плоской фигуры?
Дата добавления: 2015-09-14; просмотров: 2472;
