Правило Жуковского

Как видно из формулы (156), ускорение Кориолиса равняется удвоенному векторному произведению переносной угловой скорости и линейной относительной скорости точки.

Модуль вектора кориолисового ускорения определим по правилам нахождения модуля векторного произведения:

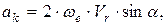(158)

где 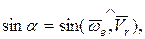то есть 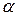– угол между векторами переносной угловой скорости и относительной скорости 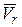точки.

Из формулы (158) видно, что коріолісове ускорение будет равняться нулю в таких случаях:

- когда 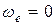, то есть, когда переносное движение является поступательным или, если переносная угловая скорость в данный момент времени превращается в нуль;

- когда 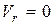, то есть движение точки не является сложным, или если относительная скорость точки в данный момент времени является нулевой;

- когда 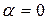или 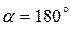, то есть когда вектор относительной скорости точки является параллельным осе вращения подвижной системы отсчета (тела).

Направление кориолисового ускорения определяется направлением векторного произведения векторов и 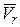, то есть коріолісове ускорение будет направлено перпендикулярно плоскости векторов и 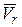в направлении, откуда поворот на меньший угол от к 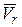видно таким, которое происходит против хода часовой стрелки (рис. 109).

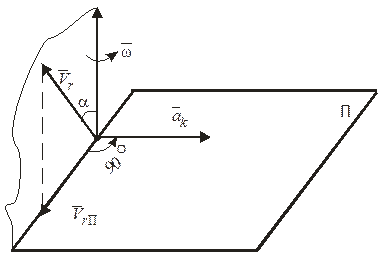
Рисунок 109

По правилу Жуковского для нахождения направления коріолісового ускорения необходимо спроектировать вектор относительной скорости 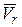на плоскость П, перпендикулярную к оси переносного вращения, а затем повернуть эту проекцию 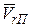на угол 90о в направлении переносного вращения (см. рис. 109).