Примеры решения задач сложного движения точки
При решении задач кинематики сложного движения точки важным является правильное деление абсолютного движения точки на относительную и переносную составляющие. Для установления вида относительного движения точки нужно мысленно остановить переносное движение (движение тела, которым двигается точка), а для установления характера переносного движения мысленно останавливают относительное движение точки.
Кинематические характеристики переносного движения следует определить по правилам нахождения соответствующих характеристик точек твердого тела.
При нахождении относительной скорости и относительного ускорения точки подвижную систему координат следует считать неподвижной и применять формулы кинематики точки.
При использовании формулы (157) для определения абсолютного ускорения точки следует помнить, что в случае поступательного переносного движения эта формула упрощается к виду
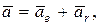 (159)
(159)
так как Кориолисово ускорение при этом равняется нулю.
Пример 21
На тележке А, который двигается из состояния покоя за горизонталью вправо с постоянным ускорением 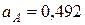 м/с2 (рис. 110), размещен электродвигатель, ротор которого вращается за законом
м/с2 (рис. 110), размещен электродвигатель, ротор которого вращается за законом 
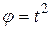 радиан. Радиус ротора
радиан. Радиус ротора 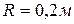 . Определить абсолютную скорость и абсолютное ускорение точки М, которая лежит на ободе ротора, в момент времени t = 1c, если в этот момент точка М находится в положении, показанном на рисунку 110.
. Определить абсолютную скорость и абсолютное ускорение точки М, которая лежит на ободе ротора, в момент времени t = 1c, если в этот момент точка М находится в положении, показанном на рисунку 110.
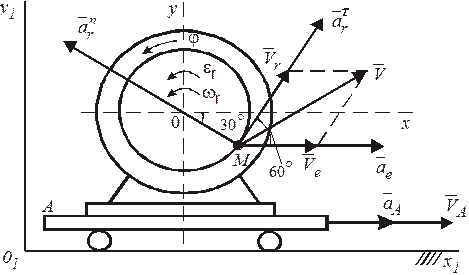
Рисунок 110
Решение
Для точки М ободу ротора поступательное движение тележки является переносным, а вращение ротора вокруг его оси является относительным. Выберем неподвижную систему отсчета O1x1y1, а подвижную систему Oxy свяжем с подвижной тележкой. Абсолютным будет движение точки М в отношении к неподвижной системе O1x1y1.
Абсолютную скорость точки М определим за зависимостью (151)
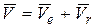 .
.
Переносная скорость точки М равняется скорости тележки в его прямолинейном поступательном равноускоренном движении. Так, как начальная скорость тележки 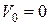 , то
, то 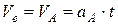 , и при времени
, и при времени 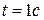 скорость
скорость 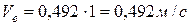 . Вектор
. Вектор 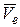 направлен параллельно осе
направлен параллельно осе 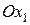 вправо. Относительную скорость найдем как скорость точки М при вращении ротора с угловой скоростью
вправо. Относительную скорость найдем как скорость точки М при вращении ротора с угловой скоростью 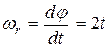 . При
. При 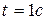 угловая скорость ротора
угловая скорость ротора 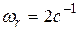 . Тогда относительная скорость
. Тогда относительная скорость 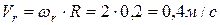 . Вектор
. Вектор 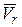 направлен перпендикулярно ОМ в направлении вращения ротора.
направлен перпендикулярно ОМ в направлении вращения ротора.
Модуль абсолютной скорости точки М определим за зависимостью (152):
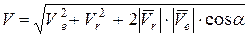 .
.
Учитывая, что угол 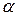 между векторами
между векторами 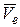 и
и 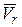 составляет 60о, одержимо
составляет 60о, одержимо
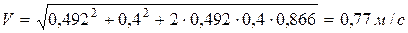 .
.
Так, как переносное движение является поступательным, то для нахождения абсолютного ускорения точки М применим зависимость (159)
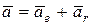 .
.
Здесь переносное ускорение равняется ускорению тележки, то есть 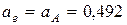 м/с2. Поскольку движение тележки ускорено, то направление вектора
м/с2. Поскольку движение тележки ускорено, то направление вектора 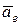 совпадает с направлением
совпадает с направлением 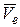 .
.
Относительное ускорение точки М при вращении ротора имеет две составляющие:
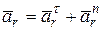 .
.
Модули этих составляющих определим за формулами касательного aф и нормального  ускорений точки тела, которое вращается:
ускорений точки тела, которое вращается:
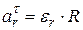 ,
, 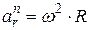 .
.
Здесь 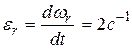 , потому касательное ускорение точки М в ее относительном движении будет иметь значение
, потому касательное ускорение точки М в ее относительном движении будет иметь значение
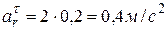 .
.
Поскольку знаки 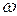 и
и 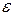 одинаковые (вращение ускорено), и векторы
одинаковые (вращение ускорено), и векторы 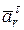 и
и 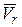 будут сонаправлеными. Нормальное ускорение точки в относительном движении будет таким:
будут сонаправлеными. Нормальное ускорение точки в относительном движении будет таким: 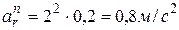 . Вектор
. Вектор 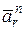 направлен к центру О вращение ротора.
направлен к центру О вращение ротора.
Величину абсолютного ускорения точки М найдем за его проекциями на осе подвижной системы координат:

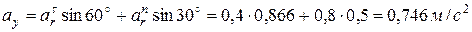 .
.
Поскольку проекция вектора абсолютного ускорения на ось х равняется нулю, то вектор 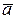 в данный момент времени направлен за вертикалью вверх.
в данный момент времени направлен за вертикалью вверх.
Дата добавления: 2015-09-14; просмотров: 3038;
