Теорема о сложении скоростей при сложном движении
Точки
| α |
Рассмотрим сложное движение точки М, которая в относительном движении перемещается относительно подвижной системы координат Oxyz и осуществляет абсолютное перемещение относительно неподвижной системы отсчетa 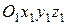 (рис. 108).
(рис. 108).
 Рисунок 108
Рисунок 108
Положение точки М в отношении к неподвижной системе координат 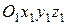 в каждый момент времени определяется зависимостью:
в каждый момент времени определяется зависимостью:
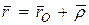 (148)
(148)
где 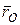 – радиус-вектор точки О начала подвижной системы координат Oxyz,
– радиус-вектор точки О начала подвижной системы координат Oxyz,
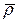 – радиус-вектор точки М в отношении к подвижной системе координат Oxyz.
– радиус-вектор точки М в отношении к подвижной системе координат Oxyz.
Считая, что координаты точки М в подвижной системе координат будут x, y, z, определим:
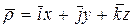 .
.
Дифференцируя зависимость (148) по времени, найдем абсолютную скорость точки
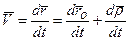 . (149)
. (149)
Абсолютная производная от вектора 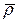 , который изменяется в подвижной системе координат, определяется формулой (147)
, который изменяется в подвижной системе координат, определяется формулой (147)
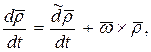
где 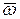 – угловая скорость вращения подвижной системы координат.
– угловая скорость вращения подвижной системы координат.
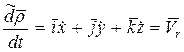 – относительная скорость точки.
– относительная скорость точки.
Подставляя эти значения в (149), получим:
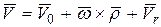 ,
,
где 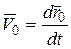 – скорость начала подвижной системы координат относительно неподвижной системы координат.
– скорость начала подвижной системы координат относительно неподвижной системы координат.
Учитывая, что переносная скорость, это скорость точки 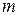 подвижной системы, через которую в данный момент проходит подвижная точка m, то есть
подвижной системы, через которую в данный момент проходит подвижная точка m, то есть
 (150)
(150)
будем иметь
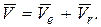 (151)
(151)
Абсолютная скорость точки при ее сложном движении равняется геометрической сумме переносной и относительной скоростей.
Направлены векторы 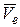 и
и 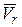 по касательным к соответствующим траекториям. Модуль абсолютной скорости точки определяется формулой
по касательным к соответствующим траекториям. Модуль абсолютной скорости точки определяется формулой
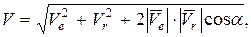 (152)
(152)
где 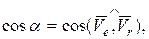 то есть a – угол между векторами
то есть a – угол между векторами 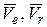 .
.
Дата добавления: 2015-09-14; просмотров: 1002;
