Движении точки

Абсолютное ускорение точки определим, дифференцируя по времени формулу (151)

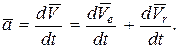(153)

Абсолютную производную вектора относительной скорости найдем за формулой (147)

.

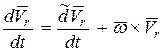В этом выражении относительная производная вектора 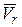по времени является ускорением точки М по отношению к подвижной системе координат, то есть относительным ускорением:

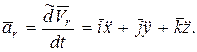
Тогда

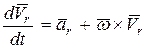. (154)

Абсолютная производная от вектора переносной скорости, согласно с формулой (150)

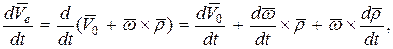
или учитывая, что 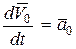– ускорение начала подвижной системы координат, 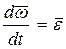– угловое ускорение подвижной системы координат, 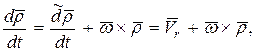получим:

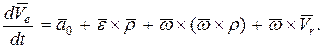
Так как переносное ускорение – это ускорение точки 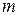тела (подвижной системы), которая совпадает с подвижной точкой М, то

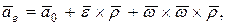
тогда

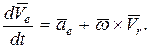(155)

Подставив (154) и (155) в (153), получим:

.

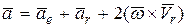Ускорение, которое определяется слагаемым 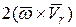,называют кориолисовым ускорение и помечают

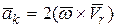. (156)

Следовательно, имеем

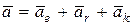. (157)

Эта формула выражает теорему Кориолиса; согласно с которой абсолютное ускорение точки при ее сложном движении равняется геометрической сумме трех ускорений: переносного, относительного и коріолісового.

Каждая из составляющих абсолютного ускорения является кинематической характеристикой изменения со временем вектора абсолютной скорости точки. Да, переносное ускорение 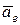- это характеристика изменения модуля и направления вектора 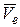переносной скорости в переносном движении, относительное ускорение 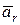характеризует изменение вектора относительной скорости 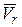в относительном движении, а коріолісове ускорение 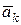появляется как характеристика изменения вектора переносной скорости в относительном движении и вектора относительной скорости в переносном движении.