Пример 22
Пластина D (рис. 111) вращается вокруг неподвижной оси за законом 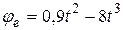 , советов. По пластине вдоль прямолинейного желоба двигается точка М соответственно закону, см.
, советов. По пластине вдоль прямолинейного желоба двигается точка М соответственно закону, см.
Найти абсолютную скорость и абсолютное ускорение точки М в момент времени  .
.

Рисунок 111
Решение
Будем считать, что в расчетный момент времени плоскость чертежа совпадает с плоскостью пластины D. Положение точки М на пластине D при  определяется расстоянием
определяется расстоянием
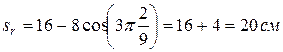 .
.
Абсолютную скорость точки М найдем как геометрическую сумму переносной и относительной скоростей:
 .
.
Относительная скорость:
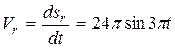 ; при
; при  имеем:
имеем: 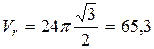 см/с.
см/с.
Положительный знак величины 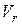 показывает, что вектор
показывает, что вектор  (рис. 112, а) направлен в сторону роста
(рис. 112, а) направлен в сторону роста  .
.
а) б)
Рисунок 112
Переносная скорость:
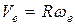 ,
,
где 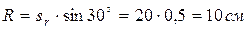 – радиус круга, который описывает та точка тела, с которой в данное мгновение совпадает точка М, а
– радиус круга, который описывает та точка тела, с которой в данное мгновение совпадает точка М, а  – угловая скорость тела.
– угловая скорость тела.
При  имеем
имеем 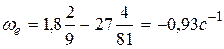 .
.
Окончательно 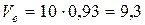 м/с.
м/с.
Отрицательный знак в величине 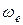 значит, что вращение треугольника вокруг оси
значит, что вращение треугольника вокруг оси 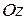 происходит противоположно направлению отсчета угла
происходит противоположно направлению отсчета угла 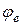 , потому вектор
, потому вектор  направлен вдоль оси
направлен вдоль оси 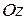 вниз (см. рис. 112, а). Вектор
вниз (см. рис. 112, а). Вектор 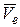 направлен за касательной к кругу радиуса R в сторону вращения тела.
направлен за касательной к кругу радиуса R в сторону вращения тела.
Так как и 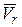 взаимно перпендикулярные, модуль абсолютной скорости точки М:
взаимно перпендикулярные, модуль абсолютной скорости точки М:
 .
.
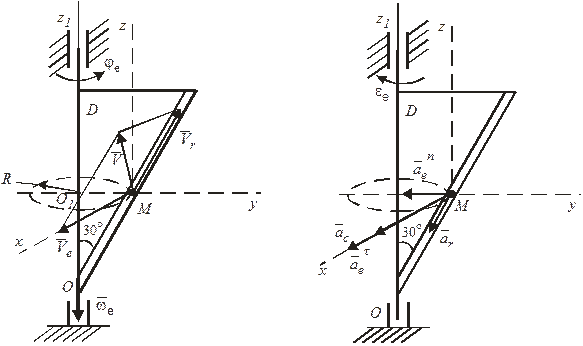
Абсолютное ускорение точки равняется геометрической сумме относительного, переносного и коріолісового ускорение:
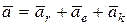 .
.
или в развернутом виде:
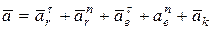 .
.
Модуль относительного касательного ускорения:
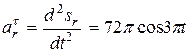 .
.
При  ;
; 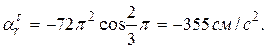
Отрицательный знак  свидетельствует, что вектор
свидетельствует, что вектор 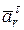 направлен в сторону отрицательных значений
направлен в сторону отрицательных значений 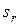 (см. рис. 112, бы).
(см. рис. 112, бы).
Относительное нормальное ускорение:
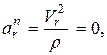
так как относительное движение точки прямолинейно.
Переносное касательное ускорение:

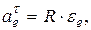
где 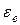 – угловое ускорение тела D.
– угловое ускорение тела D.
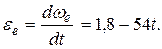
При 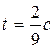

Одинаковые знаки 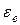 и
и 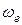 указывают на то, что вращение тела D ускорено.
указывают на то, что вращение тела D ускорено.
Тогда:

Вектор  направлен в ту сторону, что и вектор
направлен в ту сторону, что и вектор 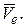
Переносное нормальное ускорение:
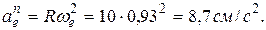
Вектор 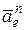 направлен к оси вращения тела D, то есть к центру О1 круга радиуса R.
направлен к оси вращения тела D, то есть к центру О1 круга радиуса R.
Ускорение Кориолиса:
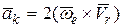 .
.
Модуль ускорения Кориолиса:
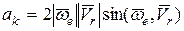
Так как 
то 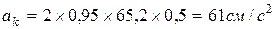 .
.
В соответствии с правилом векторного произведения вектор 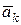 направлен перпендикулярно к плоскости треугольника D в том направлении, что и векторы
направлен перпендикулярно к плоскости треугольника D в том направлении, что и векторы  и
и  .
.
Модуль абсолютного ускорения точки М находим способом проекций векторного уравнения:
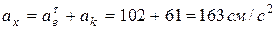 ,
,
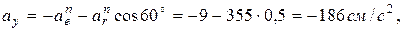
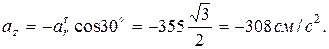
Окончательно 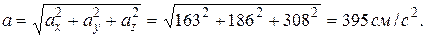
Дата добавления: 2015-09-14; просмотров: 980;
