Неопределенности и их раскрытие

Различают несколько видов неопределенностей:

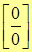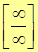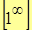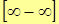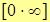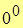, , , , , и др.

1. 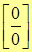. Пусть f(x₀)=0 и g(x₀)=0, тогда говорят, что 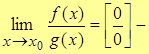неопределенность вида ноль на ноль.

а) Если числитель и знаменатель имеют одинаковые сомножители, то их можно сократить, устранив неопределенность.

Ex.1.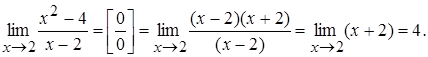

б) Если содержатся тригонометрические функции, то обычно применяют 1-й замечательный предел.

Ex.2.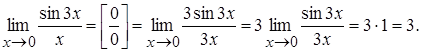

в) Если содержатся радикалы, то числитель и знаменатель умножают на «сопряженный» множитель, учитывая, что 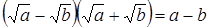и др.

Ex.3.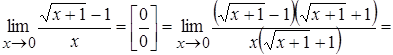

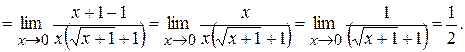
2. 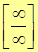. Неопределенность раскрывается делением числителя и знаменателя на алгебраическое слагаемое в максимальной степени.

3. 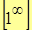. Неопределенность раскрывается применением 2-го замечательного предела.

4. 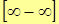. Неопределенность раскрывается приведением функций к общему знаменателю, т.е. виду 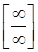или .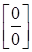

5. 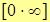. Неопределенность приводится к виду 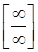или .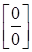

Ex. 4.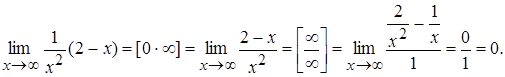

6. 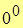. Неопределенность раскрывается предварительным логарифмированием.