Инвестиции в условиях риска. Понятие неопределенности и риска. Риски инвестиционных проектов в реальные активы
Неопределенность характеризуется множеством различных возможностей, из которых в зависимости от конкретных условий реализуется лишь одна.
Проблема неопределенности возникает в результате взаимодействия множества причин внутреннего и внешнего характера, к числу которых могут быть отнесены невозможность точно описать закономерности, цели и условия развития больших реальных систем, объектов и явлений, невозможность точно задать исходную информацию, используемую при исследованиях, и т.д.
В зависимости от вида этих причин принято различать три типа неопределенности:
– вероятностная – каждый исход имеет некоторую вероятность наступления, причем предполагается, что эти вероятности известны. Можно считать, что вероятностная неопределенность задается «поведением» самого объекта исследования, поскольку субъект здесь выступает лишь как «наблюдатель»;
– эпистемологическая – создается не только одним «поведением» объекта, но и неконтролируемой или не полностью контролируемой деятельностью исследователя;
– полная – характеризуется отсутствием всякой информации как о состоянии объекта исследования, так и о намерениях или деятельности исследователя.
Каждый тип неопределенности характеризуется определенным типом информации:
– детерминированная – однозначно характеризует события или явления;
– вероятностно-определенная – определяет случайные события или величины с известными для настоящего и будущего законами распределения вероятности;
– вероятностно-неполная – характеризует случайные события или величины, законы распределения вероятности для которых либо неизвестны, либо известны для прошлого, но не настоящего и будущего;
– неполная – отсутствие всякой информации.
Риск (или неопределенность) обусловлен вариацией ожидаемых доходов, связанных с данными инвестициями:
1. Риск – это подверженность случайным потерям, опасной случайности; опасность потерять.
2. Термин «риск» используется обычно для описания условий инвестирования, когда доход от инвестиций точно не известен, но известна совокупность альтернативных значений этого дохода и их вероятности.
3. Под условиями риска предлагается понимать множество возможных альтернативных исходов с известными вероятностями их наступления; под условиями неопределенности – то же множество возможных альтернативных исходов, но без каких-либо сведений о вероятностях их наступления.
4. Риск – не ущерб, наносимый реализацией решения, а возможность отклонения от цели, ради достижения которой принималось решение.
5. Из ситуаций неопределенности мы рассматриваем в качестве ситуаций риска такие, наступление неизвестных событий в которых весьма вероятно и может быть оценено. В то же время ситуации, когда вероятность наступления неизвестных событий мы установить заранее не можем, мы называем неопределенностью.
К числу наиболее существенных видов неопределенностей и инвестиционных рисков можно отнести:
– риск, связанный с нестабильностью экономического законодательства и текущей экономической ситуации, условий инвестирования и использования прибыли;
– внешнеэкономический риск (возможность введения ограничений на торговлю и поставки, закрытие границ и т.д.);
– неопределенность политической ситуации, риск неблагоприятных социально-политических изменений в стране или в регионе;
– неполнота и неточность информации о динамике технико-экономических показателей, параметрах новой техники и технологий;
– колебания рыночной конъюнктуры, цен, валютных ресурсов и т.д.;
– неопределенность природно-климатических условий, угроза стихийных бедствий;
– производственно-технологический риск (аварии и отказы оборудования и т.д.);
– неопределенность целей, интересов, финансового положения и поведения участников проекта (возможность неплатежей, банкротств, срыва договорных обязательств и т.д.).
Существуют различные способы количественной оценки условий риска:
Первый подход основан на использовании коэффициента риска (kz).
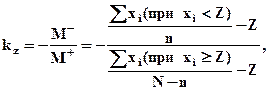
где: Z – величина планируемого показателя; N – общее число возможных значений показателя x; i = 1, ... , N; n – число показателей, для которых xi < Z; М– – ожидаемые величины показателей, меньших Z, в случае их отклонения от Z (с отрицательным знаком); М+ – ожидаемые величины показателей, больших или равных Z, в случае их отклонения от Z.
Значение kz могут находится в интервале (0, ∞). Для вычисления kz выражение удобно представить в виде:
На рисунке представлена шкала риска, которая позволяет с помощью величины kz оценить характер поведения лица, принимающего решение.
В целях более удобного пользования коэффициентами риска, для уменьшения чрезвычайно высоких значений возможно их нормирование, в результате чего их значения не выйдут за пределы интервала (0; 1). Нормированные коэффициенты риска называются индексами риска:
,
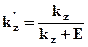где: Е > 0 – некоторое заранее выбранное постоянное число; kz' – индекс риска.
Второй подход к количественной оценке риска основан на неоклассической теории риска А. Маршалла и А. Пигу. Суть его заключается в следующем: если решение относительно выигрыша принимается в условиях риска (т.е. величина выигрыша – величина случайная), то лицо, принимающее решение, будет руководствоваться двумя критериями:
– абсолютной величиной ожидаемого выигрыша;
– размахом его возможных колебаний.
Представленная на рис. кривая безразличия характеризует закон возрастающей цены риска. По оси ординат откладывается абсолютная величина выигрыша (Хср), т.е. его математическое ожидание, по оси абсцисс – дисперсия (sх2), характеризующая разброс возможных значений выигрыша.
Следовательно, гарантированную прибыль можно выразить как дисконтированную величину ожидаемой прибыли, причем ставкой дисконта здесь является норма премии за риск, зависящая от кривой безразличия.
Можно также построить кривую безразличия для случая, когда анализируется не ожидаемый выигрыш, а ожидаемые затраты (рис. 2). Здесь отрезок ОР изображает величину гарантированных издержек, а отрезок ВР – премию за риск. Снижая издержки и получая премию за риск в размере РВ предприниматель рискует и риск количественно выражается с помощью дисперсии sх2 (отрезок 0А).
Дата добавления: 2015-08-01; просмотров: 1144;