Предел функции действительного аргумента
Пусть на плоскости с д.п.с.к. X0Y задана функция y=f(x).
| Def. 1 | Число А называют пределом функции y=f(x) в т. x0 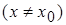 и записывают и записывают 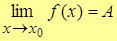 , если при любом способе стремления , если при любом способе стремления 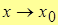 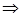 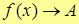 . .
|
| Def. 2 | (По Гейне[8] – на языках последовательностей)
Число А называют пределом функции y=f(x) в т. x0 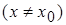 и записывают и записывают 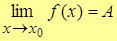 , если из сходимости последовательности аргумента , если из сходимости последовательности аргумента 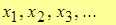 к т. x0 следует сходимость значений функции к т. x0 следует сходимость значений функции 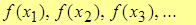 к числу А. к числу А.
|
| Def. 3 | (По Коши[9] – на языке “ε – δ ”)
Число А называют пределом функции y=f(x) в т. x0 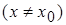 и записывают и записывают 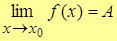 , если , если
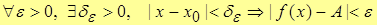 . .
|
| Def.4 | (на языке окрестностей)
Число А называют пределом функции y=f(x) в т. x0 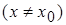 и записывают и записывают
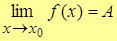 , если , если 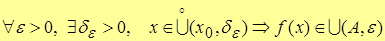 ,
где ,
где 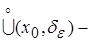 ”выколотая” окрестность т. x0; ”выколотая” окрестность т. x0;
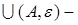 ” невыколотая” окрестность т. А. ” невыколотая” окрестность т. А.
|
| Def. 5 | (Левосторонний предел)
Число А называют левосторонним пределом функцииy=f(x) в т. x0 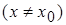 и записывают и записывают
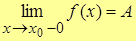 , если при , если при 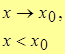 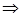 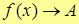 . .
|
| Def. 6 | (Правосторонний предел)
Число А называют правосторонним пределом функции y=f(x) в т. x0 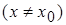 и записывают и записывают
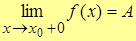 , если при , если при  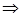 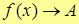 . .
|
| Note | Для функций действительного переменного справедливы все теоремы о пределах функции натурального аргумента (см. п. 5.5) |
Пусть  ,
, 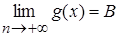 ,
,  с – const, то
с – const, то
| Т.1. |  . .
|
| Т.2. | 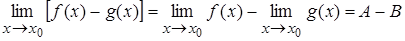 . .
|
| Т.3. | 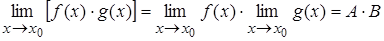 . .
|
| Т.4. |  . .
|
| Т.5. | 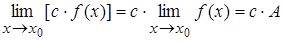 . .
|
Дата добавления: 2015-08-20; просмотров: 883;
