I. Вычисление пределов функции
1.Случай, когда при 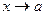 или
или 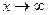 функция
функция 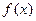 представляет отношение двух бесконечно малых величин (случай
представляет отношение двух бесконечно малых величин (случай 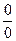 ).
).
Пример 1.1. 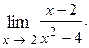
Решение. Вначале убеждаемся, что предел функции нельзя найти непосредственной подстановкой, что при указанном изменении аргумента она представляет отношение двух бесконечно малых величин (случай 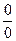 ); затем делаем преобразования, чтобы сократить дробь на множитель, стремящийся к нулю. Разлагаем знаменатель на множители и сокращаем дробь на
); затем делаем преобразования, чтобы сократить дробь на множитель, стремящийся к нулю. Разлагаем знаменатель на множители и сокращаем дробь на 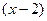 .
.
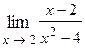 =
= 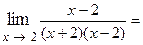
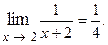
Пример 1.2. 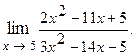
Решение.Разлагаем числитель и знаменатель дроби на множители, как квадратные трехчлены, по формуле:
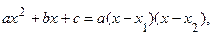
где 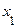 и
и 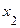 - корни трехчлена. Затем сокращаем дробь на
- корни трехчлена. Затем сокращаем дробь на  :
:
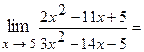
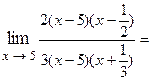
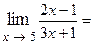
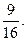
Вообще, если ищется предел дроби, числитель и знаменатель которой многочлены, обращающиеся в нуль в предельной точке  , то согласно теореме Безу оба многочлена разделяются без остатка на
, то согласно теореме Безу оба многочлена разделяются без остатка на 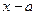 , то есть такую дробь всегда можно сократить на
, то есть такую дробь всегда можно сократить на 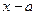 .
.
Таким образом, сократим дробь, разделив на 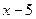 числитель и знаменатель в отдельности:
числитель и знаменатель в отдельности:
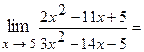
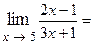
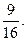
Пример 1.3. 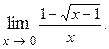
Решение. Уничтожаем иррациональность в числителе путем умножения числителя и знаменателя на 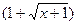 , затем сокращаем дробь на
, затем сокращаем дробь на 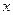 :
:
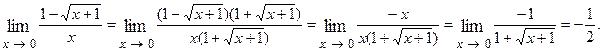
Пример 1.4. 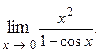
Решение. Преобразуем функцию таким образом, чтобы использовать 1-й замечательный предел:


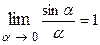 (
( 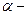 радианная мера угла).
радианная мера угла).
Применяем тригонометрическую формулу:

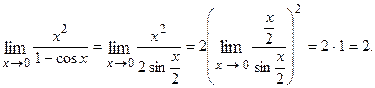
2.Случай, когда при 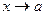 или
или 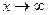 функция
функция 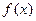 представляет отношение двух бесконечно больших величин (случай
представляет отношение двух бесконечно больших величин (случай 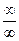 ).
).
Пример 2.1. 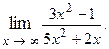
Решение.Убедившись, что имеет место случай 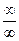 , преобразуем функцию путем деления числителя и знаменателя дроби на
, преобразуем функцию путем деления числителя и знаменателя дроби на 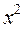 (наивысшая степень
(наивысшая степень  ):
):
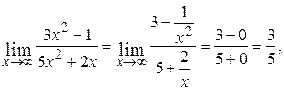
при 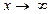 величины
величины 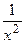 и
и 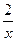 являются бесконечно малыми.
являются бесконечно малыми.
Пример 2.2. 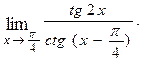
Решение. Тождественно преобразуем дробь так, чтобы затем сократить ее на множитель, стремящийся к нулю:
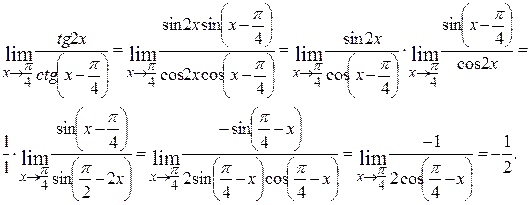
3. Случай, когда при 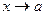 или
или 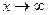 функция
функция 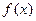 представляет произведение бесконечно малой величины на бесконечно большую (случай
представляет произведение бесконечно малой величины на бесконечно большую (случай 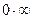 ).
).
Данный случай нахождения предела функции производится путем преобразования функции к одному из двух рассмотренных случаев, т.е. к случаю 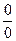 или к случаю
или к случаю 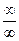 .
.
Пример 3.1. 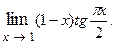
Решение. Установив, что при указанном изменении аргумента функция представляет произведение бесконечно малой величины на бесконечно большую (случай 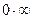 ), преобразуем её к виду дроби, числитель и знаменатель которой одновременно стремятся к нулю или к бесконечности.
), преобразуем её к виду дроби, числитель и знаменатель которой одновременно стремятся к нулю или к бесконечности.
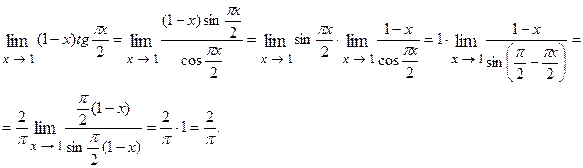
Пример 3.2. 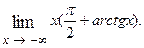
Решение. Положим 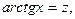 тогда
тогда 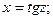
 когда
когда 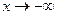 и, следовательно,
и, следовательно,
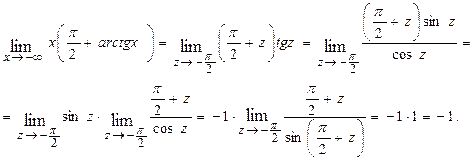

4. Случай, когда при 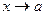 или
или 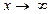 функция
функция 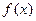 представляет разность двух положительных бесконечно больших величин (случай
представляет разность двух положительных бесконечно больших величин (случай 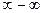 ).
).
Данный случай нахождения предела функции можно привести к случаю 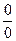 или
или 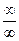 путем преобразования функции к виду дроби.
путем преобразования функции к виду дроби.
Пример 4.1. 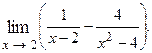
Решение. Делаем заключение, что при указанном поведении аргумента функция представляет разность двух положительных бесконечно больших величин (случай 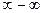 ). Преобразуем функцию к виду дроби, числитель и знаменатель которой одновременно стремятся к нулю или к бесконечности.
). Преобразуем функцию к виду дроби, числитель и знаменатель которой одновременно стремятся к нулю или к бесконечности.
Производим вычитание дробей и полученную в результате дробь сокращаем на 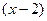 :
:
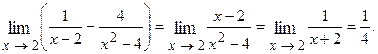
Дата добавления: 2015-07-30; просмотров: 3104;
