II. Вычисление производных функций
Таблица основных производных
| № п/п | Функция y | Производная y’ | № п/п | Функция y | Производная y’ |
| c | 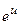
| 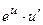
| |||
| x | 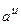
| 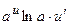
| |||
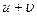
| 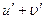
| 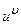
| 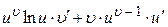
| ||
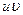
| 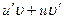
| 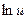
| 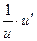
| ||

| 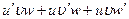
| 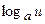
| 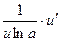
| ||

| 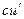
|  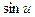
| 
| ||
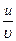
| 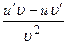
|  
| 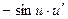
| ||
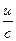
| 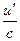
| 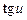
| 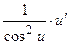
| ||
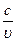
| 
| 
| 
| ||
 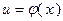
| 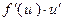
| 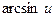
| 
| ||
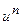
| 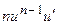
| 
| 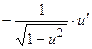
| ||
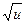
| 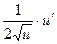
| 
| 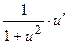
| ||
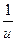
| 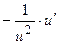
| 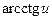
| 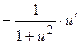
|
Пользуясь формулами и общими правилами дифференцирования, найти производные следующих функций:
2.1. 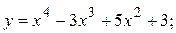 2.2.
2.2. 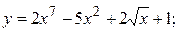
2.3. 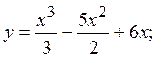 2.4.
2.4. 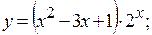
2.5. 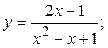 2.6.
2.6. 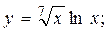
2.7. 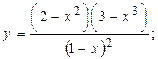 2.8.
2.8. 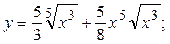
2.9. 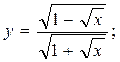 2.10.
2.10. 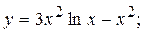
2.11. 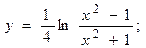 2.12.
2.12. 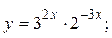
2.13. 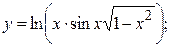 2.14.
2.14. 
2.15. 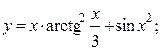 2.16.
2.16. 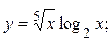
2.17. 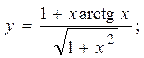 2.18.
2.18. 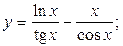
2.19. 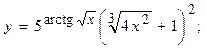 2.20.
2.20. 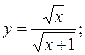
2.21. 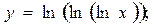 2.22.
2.22. 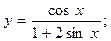
2.23. 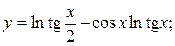 2.24.
2.24. 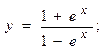
2.25. 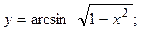 2.26.
2.26. 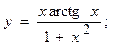
2.27. 
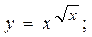 2.28.
2.28. 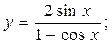
2.29. 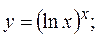 2.30.
2.30. 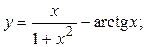
2.31. 
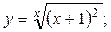 2.32.
2.32. 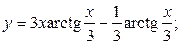
2.33. 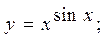 2.34.
2.34. 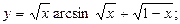
2.35. 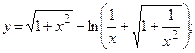 2.36.
2.36. 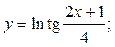
2.37. 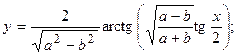 2.38.
2.38. 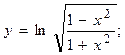
2.39. 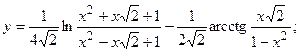 2.40.
2.40. 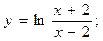
2.41.  ; 2.42.
; 2.42. 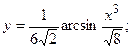

2.43. 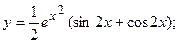 2.44.
2.44. 
2.45. 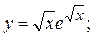 2.46.
2.46. 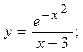
2.47. 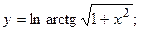 2.48.
2.48. 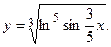
Для нахождения производных показательно-степенных и некоторых алгебраических функций полезно бывает предварительно прологарифмировать функцию.
Пример 2.1. 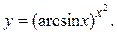
Решение. Прологарифмируем заданную функцию, а затем найдем ее производную:
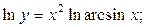
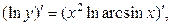

откуда 
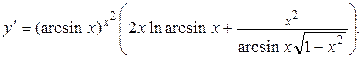
Пример 2.2. 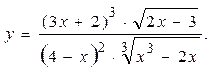
Дата добавления: 2015-07-30; просмотров: 2361;
