Частные производные функции многих переменных. Градиент.
Переменная 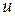 называется функцией
называется функцией 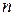 переменных (аргументов)
переменных (аргументов)  , если каждой системе значений
, если каждой системе значений  , из области их изменения, соответствует определенное значение
, из области их изменения, соответствует определенное значение 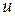 .
.
Функциональная зависимость 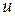 от
от  символически обозначается:
символически обозначается:  .
.
Геометрически каждая система значений двух переменных 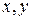 изображается точкой на плоскости, а функция двух переменных
изображается точкой на плоскости, а функция двух переменных 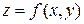 - некоторой поверхностью в пространстве; система значений трех переменных
- некоторой поверхностью в пространстве; система значений трех переменных 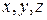 изображается точкой в пространстве. Систему значений любого числа
изображается точкой в пространстве. Систему значений любого числа 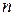 переменных
переменных  называют точкой
называют точкой 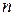 -мерного пространства
-мерного пространства 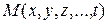 , а функцию
, а функцию 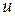 , зависящую от
, зависящую от 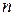 переменных, называют функцией точки
переменных, называют функцией точки 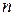 -мерного пространства
-мерного пространства 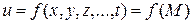 .
.
Частной производной от функции 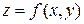 по независимой переменной
по независимой переменной 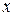 называется конечный предел
называется конечный предел
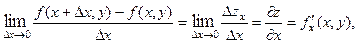
вычисленный при постоянном значении 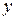 .
.
частной производной по 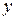 называется конечный предел
называется конечный предел
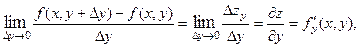
вычисленный при постоянном значении 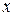 .
.
Для вычисления частных производных можно воспользоваться обычными правилами и формулами дифференцирования.
Пример 2.3.Найти 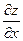 и
и 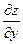 , если
, если 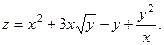
Решение.При вычислении 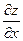 переменная
переменная 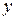 рассматривается как постоянная величина:
рассматривается как постоянная величина:
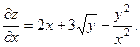
Рассмотрим теперь переменную 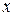 как постоянную величину:
как постоянную величину:
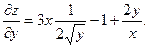
Найти частные производные от функций:
2.54. 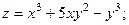 2.55.
2.55. 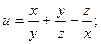
2.56. 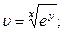 2.57.
2.57. 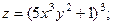
2.58.  2.59.
2.59. 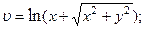
2.60. 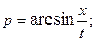 2.61.
2.61. 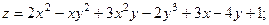
2.62. 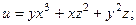 2.63.
2.63. 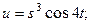
2.64. 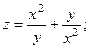 2.65.
2.65. 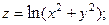
2.66. 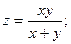 2.67.
2.67. 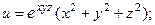
2.68. 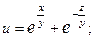 2.69.
2.69. 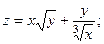
2.70. 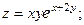 2.71.
2.71. 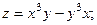
2.72. 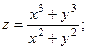 2.73.
2.73. 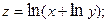
2.74. 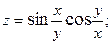 2.75.
2.75. 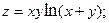
2.76. 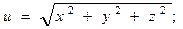 2.77.
2.77. 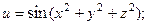
2.78. 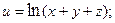 2.79.
2.79. 
Пример 2.4.Показать, что функция 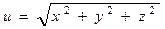 удовлетворяет уравнению
удовлетворяет уравнению 
Решение.Находим
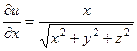 (при постоянных
(при постоянных 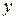 и
и 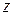 );
);
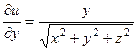 (при постоянных
(при постоянных 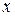 и
и 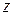 );
);
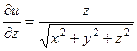 (при постоянных
(при постоянных 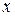 и
и 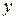 ).
).
Возводим полученные выражения в квадрат и подставляем в левую часть заданного уравнения:
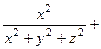

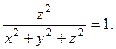
Получаем тождественное равенство, т.е. функция u удовлетворяет заданному уравнению.
Показать, что данные функции удовлетворяют приведенным уравнениям:
2.80. 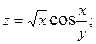
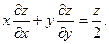
2.81. 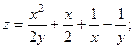
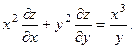
2.82. 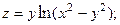
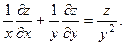
2.83. 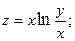
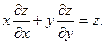
2.84. 
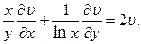
2.85. 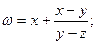
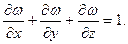
Градиентомфункции 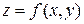 в точке
в точке 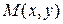 называется вектор с началом в точке
называется вектор с началом в точке 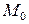 , координаты которого равны соответствующим частным производным
, координаты которого равны соответствующим частным производным 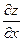 и
и 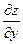 , вычисленным в точке
, вычисленным в точке  . Градиент обозначается
. Градиент обозначается 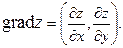 Аналогично определяется градиент и для функции трех переменных.
Аналогично определяется градиент и для функции трех переменных.
Пример 2.5.Найти градиент функции 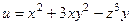 в точке М(-2;3;-1).
в точке М(-2;3;-1).
Решение.Находим частные производные данной функции:
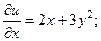

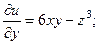
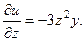
Вычисляем значение этих производных в точке М(-2;3;-1):
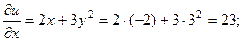
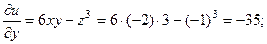
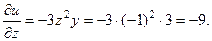
Окончательно получаем grad u(M)=(23; -35; -9).
Найти градиент функции:
2.86. 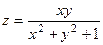 в точке М(0; 3). 2.87.
в точке М(0; 3). 2.87. 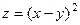 в точке М(1; 1).
в точке М(1; 1).
2.88. 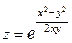 в точке М(1; 1). 2.89.
в точке М(1; 1). 2.89. 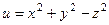 точке М(2; 0; 3).
точке М(2; 0; 3).
2.90. 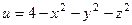 в точке М(3; 2; 1).
в точке М(3; 2; 1).
2.91. 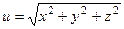 в точке М(3; -1; 2).
в точке М(3; -1; 2).
2.92.  точке М(a; b; c).2.93.
точке М(a; b; c).2.93. 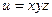 точке М(3; -1; 2).
точке М(3; -1; 2).
Дата добавления: 2015-07-30; просмотров: 1876;
