Формула Ньютона – Лейбница
Теорема.Пусть функция 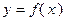 непрерывна на отрезке
непрерывна на отрезке 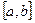 и
и 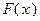 - любая первообразная для
- любая первообразная для 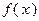 на
на 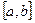 . Тогда определенный интеграл от функции
. Тогда определенный интеграл от функции 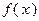 на
на 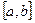 равен приращению первообразной
равен приращению первообразной 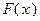 на этом отрезке, т.е.
на этом отрезке, т.е.
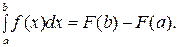
Нахождение определенных интегралов с помощью формулы Ньютона – Лейбница осуществляется в два этапа: 1) используя методы вычисления неопределенного интеграла, находят некоторую первообразную F(x) для подынтегральной функции f(x); 2) применяя собственно формулу Ньютона – Лейбница, находят приращение первообразной, равное искомому интегралу.
Пример 5.1.Вычислить 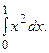
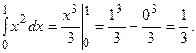
Дата добавления: 2015-07-30; просмотров: 1362;
