Формула интегрирования по частям для определенного интеграла
Теорема.Пусть функции 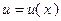 и
и 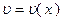 имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке 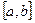 . Тогда
. Тогда
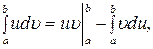
где 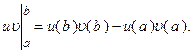
Пример 5.3.Вычислить 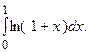
Пусть 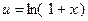 ,
,  . Тогда
. Тогда 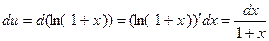 и
и 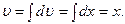 Применяя формулу интегрирования по частям, получаем
Применяя формулу интегрирования по частям, получаем
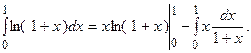 Полученный интеграл находим методом замены переменной. Пусть
Полученный интеграл находим методом замены переменной. Пусть  , тогда
, тогда  ,
, 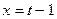 и если
и если  , то
, то 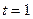 , если
, если 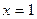 , то
, то 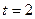 . Следовательно,
. Следовательно,
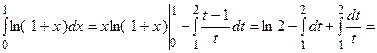
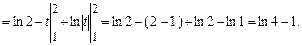
Вычислить определенные интегралы:
5.1. 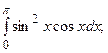 5.2.
5.2. 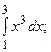
5.3. 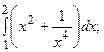 5.4.
5.4. 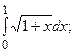
5.5.  5.6.
5.6. 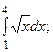
5.7. 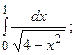 5.8.
5.8. 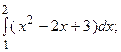
5.9. 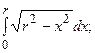 5.10.
5.10. 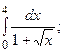
5.11.  5.12.
5.12. 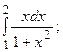
5.13. 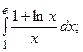 5.14.
5.14. 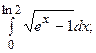
5.15. 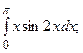 5.16.
5.16. 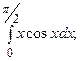
5.17. 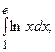 5.18.
5.18. 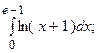
5.19. 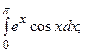 5.20.
5.20. 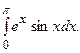
Дата добавления: 2015-07-30; просмотров: 1262;
