Пример 4.2.
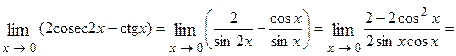
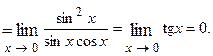
5. Случай, когда при 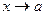 или
или 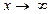 функция
функция 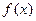 представляет степень, основание которой стремится к единице, а показатель – к бесконечности (случай
представляет степень, основание которой стремится к единице, а показатель – к бесконечности (случай  ).
).
В данном случае для нахождения предела функции используется 2-й замечательный предел:
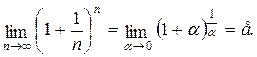
е = 2,7182818… - основание натурального логарифма ln.
Пример 5.1. 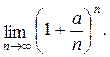
Решение. При указанном изменении аргумента функция представляет степень, основание которой стремится к единице, а показатель – к бесконечности (случай 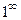 ). Преобразуем функцию таким образом, чтобы использовать 2-й замечательный предел. Полагаем
). Преобразуем функцию таким образом, чтобы использовать 2-й замечательный предел. Полагаем 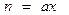 , получим, что при
, получим, что при 
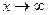 :
:
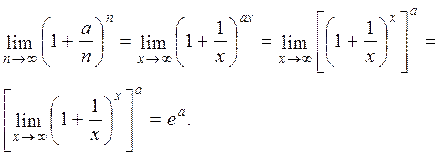
Пример 5.2. 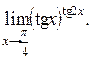
Решение. Полагаем  получим, что при
получим, что при 
 .
.

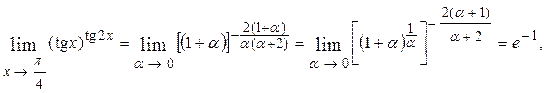
так как 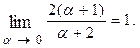
6.Вычисление предела функции по правилу Лопиталя.
Предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных, если он существует, или равен бесконечности.
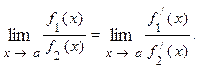
Правило Лопиталя можно применять последовательно несколько раз, если это полезно, до получения результата.
Пример 6.1. 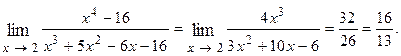
Пример 6.2. 
В примере 6.2 правило Лопиталя применено дважды.
Найти следующие пределы:
1.1. 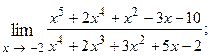 1.2.
1.2. 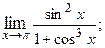
1.3. 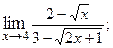 1.4.
1.4. 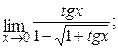
1.5. 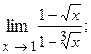 1.6.
1.6. 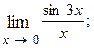
1.7. 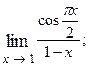 1.8.
1.8. 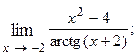
1.9. 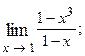 1.10.
1.10. 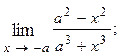
1.11. 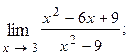 1.12.
1.12. 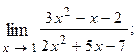
1.13. 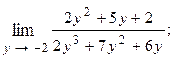 1.14.
1.14. 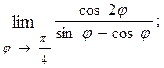

1.15. 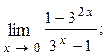 1.16.
1.16. 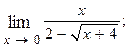
1.17. 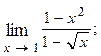
 1.18.
1.18. 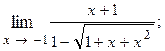
1.19. 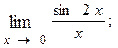 1.20.
1.20. 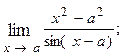
1.21. 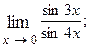 1.22.
1.22. 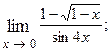
1.23.  1.24.
1.24. 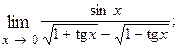
1.25. 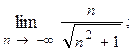 1.26.
1.26. 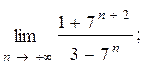
1.27. 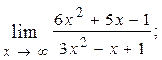 1.28.
1.28. 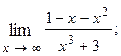
1.29.  1.30.
1.30. 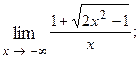

1.31. 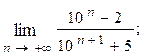 1.32.
1.32. 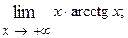
1.33. 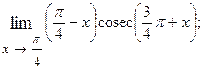 1.34.
1.34. 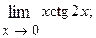
1.35. 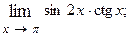 1.36.
1.36. 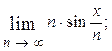
1.37. 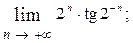 1.38.
1.38. 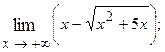
1.39. 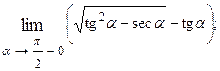 1.40.
1.40. 
1.41. 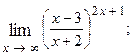
 1.42.
1.42. 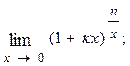
1.43. 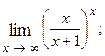 1.44.
1.44. 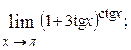
1.45. 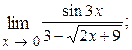 1.46.
1.46. 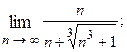
1.47. 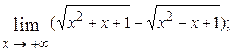 1.48.
1.48. 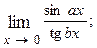
1.49.  1.50.
1.50. 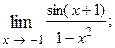
1.51. 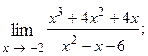 1.52.
1.52. 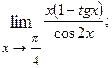
1.53. 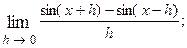 1.54.
1.54. 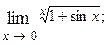
1.55. 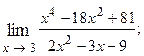 1.56.
1.56. 
1.57. 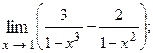 1.58.
1.58. 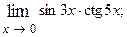
1.59. 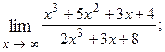 1.60.
1.60. 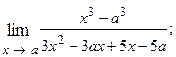
1.61. 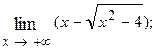 1.62.
1.62. 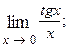
1.63. 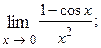 1.64.
1.64. 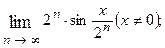
1.65. 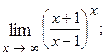 1.66.
1.66. 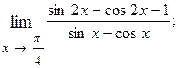
1.67. 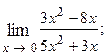 1.68.
1.68. 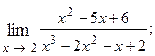
1.69. 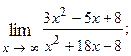 1.70.
1.70. 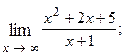
1.71. 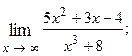 1.72.
1.72. 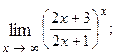
1.73. 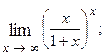 1.74.
1.74. 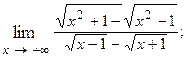
1.75. 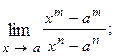 1.76.
1.76. 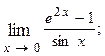
1.77. 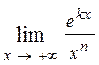 (k>0, n – натуральное число); 1.78.
(k>0, n – натуральное число); 1.78. 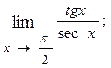
1.79. 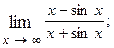 1.80.
1.80. 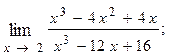
1.81.  1.82.
1.82. 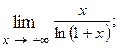
1.83. 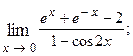 1.84.
1.84. 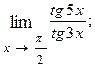
1.85. 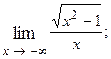 1.86.
1.86. 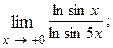
1.87. 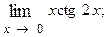 1.88.
1.88. 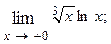
1.89. 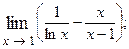 1.90.
1.90. 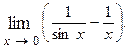
Дата добавления: 2015-07-30; просмотров: 1291;
