Аппроксимация аналитических функций полиномами.
Пусть 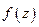 аналитическая функция в окрестности
аналитическая функция в окрестности 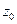 , тогда всюду в круге
, тогда всюду в круге 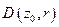
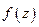 равномерно приближается полиномом.
равномерно приближается полиномом.
 Можно разложить
Можно разложить 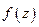 в ряд Тейлора в окрестности
в ряд Тейлора в окрестности 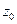
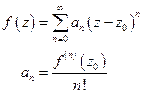
- ряд сходится в круге сходимости 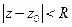 ,
, 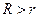
- ряд сходится в круге 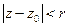
Поэтому в качестве приближающих полиномов можно взять полиномы Тейлора – частичные суммы ряда Тейлора
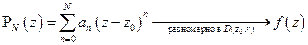
Если 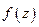 аналитична в некоторой области
аналитична в некоторой области 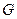 , то можно ли приблизить нашу функцию полиномами?
, то можно ли приблизить нашу функцию полиномами?
Пусть 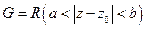 - кольцо.
- кольцо.
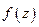 аналитична в
аналитична в 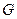 , тогда
, тогда 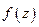 раскладывается в ряд Лорана
раскладывается в ряд Лорана
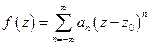
Если  , то слагаемые имеют вид
, то слагаемые имеют вид 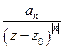 - можно ли полиномом приблизить эту функцию?
- можно ли полиномом приблизить эту функцию?
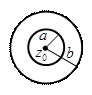 в кольце не можем приблизить полиномами вида
в кольце не можем приблизить полиномами вида 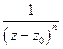 ,
, 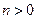
Рассмотрим функцию 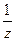 на единичной окружности
на единичной окружности 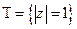 .
.
Требуется найти последовательность полиномов 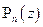 так, чтобы
так, чтобы 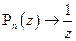 на
на 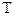 :
:
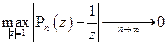
Теорема. Такой последовательности полиномов не существует.
Доказательство: Докажем, что 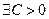 , что
, что
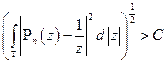
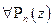
Допустим, что такую константу нашли, тогда
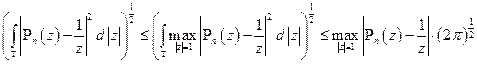
Докажем существование константы 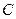
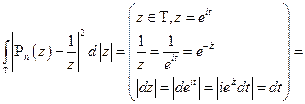
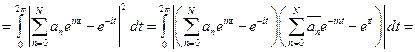
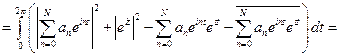
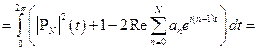
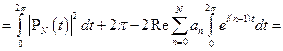
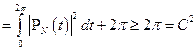
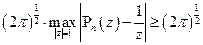
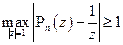
Дата добавления: 2015-07-24; просмотров: 1327;
