Принцип аргумента
Пусть 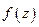 мероморфная функция в
мероморфная функция в 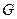 (могут быть полюса).
(могут быть полюса).
Тогда
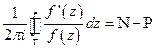 ,
,
где 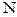 - число нулей функции
- число нулей функции 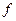 внутри области с учетом кратности,
внутри области с учетом кратности,
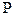 - аналогичное число полюсов.
- аналогичное число полюсов.
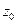 - нуль кратности
- нуль кратности 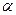 , то
, то 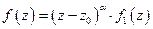 ,
, 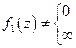
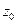 - полюс кратности
- полюс кратности 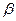 , то
, то 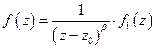 ,
, 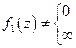
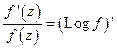 - логарифмическая производная.
- логарифмическая производная.
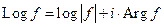 - многозначная функция.
- многозначная функция.
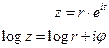
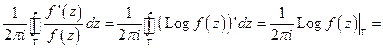
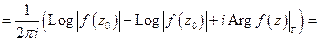
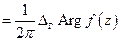 - приращение аргумента.
- приращение аргумента.
Величина 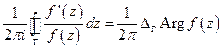 - индекс функции
- индекс функции 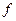 по кривой
по кривой 
(индекс считает число оборотов при обходе кривой  )
)
Доказательство: 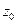 - корень кратности
- корень кратности 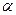
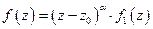
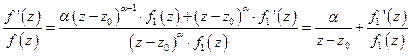
По теореме о вычетах
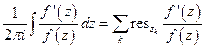
(сумма распространяется на все особые точки функции 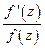 ).
).
Какие особые точки у функции 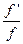 ?
?
Если 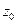 - корень
- корень 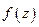 , то
, то 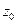 - особая точка
- особая точка 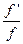
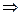
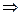
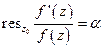 ,
, 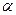 - кратность корня.
- кратность корня.
Если 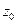 - полюс кратности
- полюс кратности 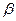
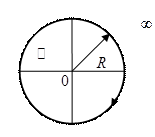
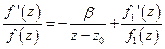
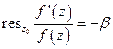
Потом надо просуммировать все вычеты.
Вычет функции в бесконечной точке ( 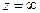 ).
).
Если 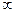 - изолированная особая точка
- изолированная особая точка
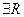 :
: 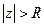 нет других особых точек
нет других особых точек
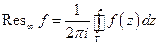
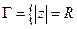 , что при
, что при 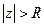 нет других особых точек, и интегрируем в положительном направлении относительно
нет других особых точек, и интегрируем в положительном направлении относительно 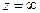
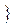
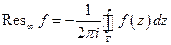
Дата добавления: 2015-07-24; просмотров: 783;
