Следствие из принципа аргумента

Пусть 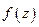аналитична вне кривой , тогда

Пусть число нулей с учетом кратностей 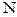, тогда

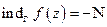
Если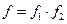

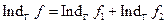
Формулировка задачи Римана:

Пусть 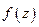, 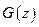- функция на 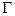(замкнутая).

Требуется найти две аналитических функции

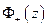внутри ,

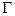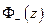вне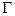

так, чтобы выполнялось:

o Для предельных значений на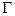

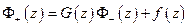
o Однородная задача Римана ( )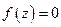

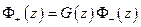
I шаг. ,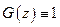

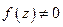
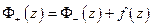
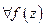(непрерывность по Гёльдеру)

Рассмотрим интеграл Коши

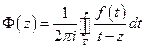
По формулам Сохоцкого

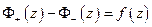
II шаг. Пусть имеем решение однородной задачи

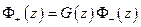
Найдем индексы от обеих частей равенства

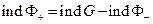
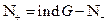
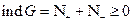
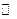
1.) 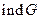, предположим, что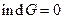

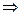
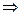функция 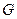однозначна, существует .

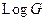Решим задачу

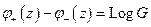
По формулам Сохоцкого

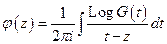
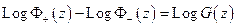
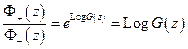
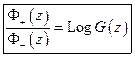
2.) 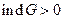( 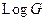- неоднозначная функция)

Обозначим 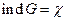, тогда

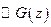
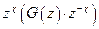
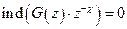
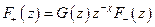
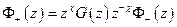
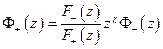
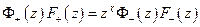
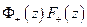- аналитична внутри, 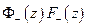- аналитична вне

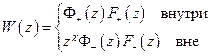
аналитична во всей плоскости 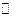, на 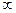у неё полюс порядка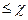

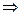
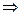
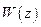- полином.