Теорема Рунге

Если 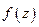аналитична в 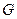со связным дополнением, то 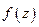равномерно приближается полиномами в любой области 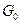, компактно содержащейся в .

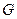Доказательство:

I шаг. Докажем, что любую аналитическую 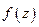в области 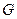можно приблизить рациональными функциями.

Рассмотрим интеграл Коши по границе области 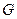, тогда

,

, :

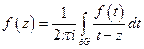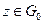
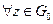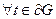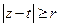
Представим интеграл в виде Римановой суммы

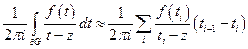
Подынтегральная функция 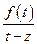- непрерывна и ограничена, тогда суммы Римана сходятся к интегралу если ранг разбиения стремится к нулю.

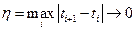
Поэтому если 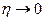, то

,

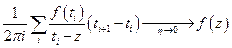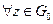
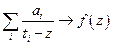
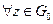
т.е. доказали, что последовательность рациональных функций сходится к .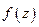

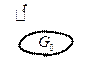II шаг. Надо приблизить полиномом в области 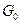функцию 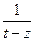, где , , .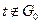

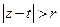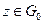Обозначим через 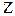- множество тех 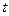, что функции вида 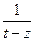приближаются полиномами на множестве .

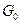Надо выяснить что за множество 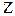. Оказывается 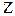- дополнение 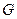до всей плоскости ( ).

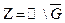Пусть 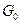содержится в круге радиуса ,

,

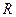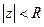
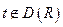
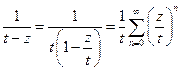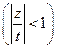
т.е. 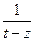разложим в ряд Тейлора в круге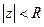

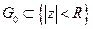
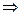ряд Тейлора сходится во всех 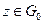, и приближающие полиномы – это полиномы Тейлора.

а) Кроме того, множество 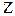- замкну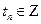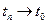то ( , , то )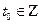

Если 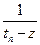- приближается полиномами, то 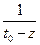тоже приближается;

б) 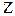- открыто 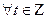существует 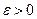, что 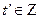, если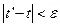

Если 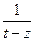- приближается, то и функция 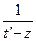тоже приближается.

Множество 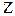- открытое замкнутое не пустое, значит совпадает со всем дополнением множества .

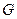Определение связного множества.

Если множество 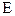нельзя разбить в объединение двух непересекающихся одновременно открытых и замкнутых множеств, то 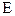- связно.

Комментарии.

Если известно, что 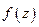аналитическая функция в 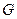(со связным дополнением), то можно найти полином : .

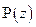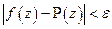Если 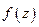- произвольная функция на границе области, то в общем случае аналитического полинома нет.

Зато для любой непрерывной 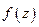на границе существует гармонический полином, который приближает 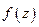на границе.