Аксиоматическая теория действительных чисел. Построение модели. Свойства действительных чисел. Теорема существования корня

5. Бинарные отношения. Отношение эквивалентности, разбиение на классы, фактор-множество

Бинарные отношения. Для любых двух множеств X и Y всякое подмножество ω  X*Y называется бинарным отношениеммежду X и Y (или просто на Х, если Y=X). Для упорядоченной пары (x,y)ω используют обозначение x ω y и говорят, что x находится в отношении ω к y. Это удобно, поскольку, например, упорядочение < на множестве вещественных чисел R является бинарным отношением на R, состоящим из всех точек плоскости R², которые лежат выше прямой x–y=0 (рис.1); громоздкое включение (х,у)ω(ω) заменяется обычным неравенством ху.

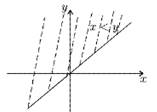
Каждой функции f: ХY сопоставляется ее график – подмножество Г(f)={(x,y)|xX,y=f(x)}X*Y, являющееся отношением между X и Y.

Не каждое отношение ω может служить графиком какого-либо отображения XY. Необходимое и достаточное условие заключается в том, чтобы каждому xX отвечал ровно один элемент y  xωy. Фактически задание X, Y и графика Г(f) восстанавливает f.

Отношение эквивалентности. Бинарное отношение ~ на Х называется отношением эквивалентности, если для всех х, х`, х``Х выполнены условия:

1)х~х (рефлексивность);

2)х~х`=>x`~x (симметричность);

3) х~х`, х`~х``=>x~x`` (транзитивность).

Подмножество 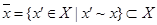всех элементов, эквивалентных данному х, называется классом эквивалентности, содержащим х. Так как х~х (условие 1), то действительно 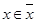. Любой элемент называется представителем класса .

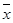Справедливо следующее утверждение:

Множество классов эквивалентности по отношению ~ является разбиением множества Х в том смысле, что Х является объединением непересекающихся подмножеств.

В самом деле, так как , то . Если теперь 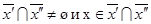, то х~х` и х~х``, откуда в силу транзитивности условия 3 имеем х`~х`` и 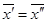. Значит, различные классы не пересекаются.

Пусть П= R² – вещественная плоскость с прямоугольной системой координат.

Взяв за свойство ~ принадлежность точек Р, P`П одной горизонтальной прямой, мы получим отношение эквивалентности с классами – горизонтальными прямыми (рис.2).

Гиперболы Г_ρ (рис.3) вида ху=ρ>0 определяют отношение эквивалентности в области П₊П точек Р(х,у) с координатами х>0, y>0. эти примеры показывают, что верно следующее обратное утверждение:

Если имеется какое-то разбиение π(Х) множества Х на непересекающиеся подмножества С_х, то С_х будут классами эквивалентности по некоторому отношению эквивалентности ~.

В самом деле, по условию каждый элемент хХ содержится точно в одном подмножестве С_α. Достаточно считать х~х`в том и только в том случае, когда х и х` лежат в одном и том же подмножестве С_α. Очевидно, это отношение ~ рефлексивно, симметрично и транзитивно, т.е. является отношением эквивалентности. Далее, х С_α=> 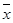= С_α по определению ~. Стало быть, π(Х)= π_~(Х).

Факторизация отображений. Ввиду установленного взаимно однозначного соответствия между отношениями эквивалентности и разбиениями множества Х принято разбиение, отвечающее отношению эквивалентности ~, обозначать Х/~ и называть фактор-множеством Х относительно ~ (или по отношению ~). Сюръективное отображение называется естественным отображением (или канонической проекцией) Х на фактор-множество Х/~.