Группа, кольцо, поле. Простейшие свойства поля. Поле рациональных чисел. Упорядоченное поле
Алгебраической структурой называется множество, на котором задана одна или несколько алгебраических операций.
<A, *, °, □>
Группы. Алгебраическая структура <G, *>, где * - бинарная алгебраическая операция на G, называется группой, если:
* - ассоциативная операция, т.е. a*(b*c)=(a*b)*c;
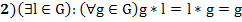, т.е. в G сущ. нейтральный элемент относительно этой операции;
3) 
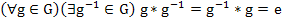существует симметричный элемент.
Если «+» g+g-1=0 (обычно g-1)=(-g)); g+(-g)=-g+g=0, то говорят, что g – противоположный элемент. Вместо симметричного, говорят, что элемент обратный.
Примеры: рассмотрим множество Z относительно операции сложения
<Z, +> – абелева группа
«+» - ассоциативна;
0 – нейтральный элемент
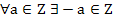a+(-a)=0
Если в группе G операция * коммутативна, то такая группа называется коммутативной или абелевой.
Также абелевыми группами являются: множество <Q, +>; <R, +>; <C, +> (рациональных, действительных и комплексных чисел)
<Z, ×> не является группой, т.к. нарушено 3 условие (2×½=1, но ½ є Z)
<Q, ×> не группа, т.к. не существует обратного элемента для нуля
<Q\{0}, ×> группа (необходимо выбросить 0, для того чтобы рациональные числа «×» были группой).
Кольца. Множество, в котором заданы 2 алгебраические операции «+» и «×» наз. кольцом, если:
1)относительно «+» это множество является абелевой группой <K, +>;
2) «+» и «×» связаны законом дистрибутивности, т.е. (a+b)c=ac+bc (правый закон дистрибутивности) и с(a+b)=ca+cb (левый закон дистрибутивности)
Если «×» коммутативно, то кольцо <K, +, ×> тоже называется коммутативным.
Если «×» ассоциативно, то кольцо <K, +, ×> называется ассоциативным.
Пример: <Z, +, ×> - коммутативное и ассоциативное кольцо.
1)<Z, +> - абелева группа, т.к. «+» коммутативно (a=b)=(b+a) и ассоциативно a+(b+c)=(a+b)+c
0 є Z и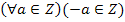 
2)ab=ba умножение коммутативно; a(bc)=(ab)c – ассоциативно
(a+b)c=ac+bc=c(a+b)=ca+cb
Другие примеры: <Q, +, ×>, <R, +, ×>, <C, +, ×>
Не коммутативным, но ассоциативным кольцом является кольцо квадратных матриц.
Рассмотрим матрицу 2-го порядка:
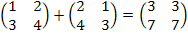<K, +> абелева группа; выполняется дистрибутивность относительно сложения
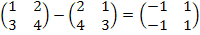
<M2×2, +> абелева группа (множество матриц по сложению)
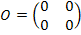– нулевая матрица
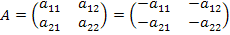– противоположная матрица
≠ 
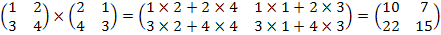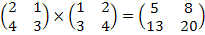
AB≠BA, но A(BC)=(AB)C
Умножение матриц дистрибутивно относительно сложения: (A+B)C=AC+BC и C(A+B)=CA+CB
В кольцах могут быть делители нуля – это такие элементы a≠0, b≠0, но ab=0.
Существуют кольца как с делителями нуля, так и без делителей нуля. В полях делителей нуля нет.
<P, +, ×> - поле и a,b≠0; a,b є P
если a×b=0
для a≠0 bP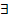 
a-1
a-1(ab)=a-1×0
(a-1×a)b=0
b=0
Если mod простой, то делителей нуля нет.
Делители нуля есть в кольцах матриц: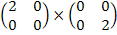 
= 
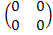
Поля. Коммутативное и ассоциативное кольцо с единицей называется полем, если для каждого ненулевого элемента есть обратный.
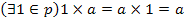
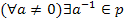
Наименьшим числовым полем является поле рациональных чисел. Q={x=p/q, pєZ, qєN}
Полями также являются действительные (R) и комплексные (С) числа.
Характеристикой поля называется такое натуральное наименьшее число nєN, что если l=1, то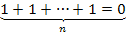 
, если такого n не существует, то это поле характеристики 0 (бесконечное поле).
Числовое множество, в котором есть 1 и в котором выполнимы операции «+», «×» и «-», «:» кроме (:0) называется числовым полем.
Полями характеристики 0 являются числовые поля Q, R, C.
Z/p, p – простое число.
Множество классов вычетов по простому полю является полем характеристики p. Поле характеристики p – p различных элементов.
Простейшие свойства поля. Пусть a, b – элементы поля F и b0. Уравнение bx=a имеет в поле решение ab-1; легко проверить, что ab-1 является единственным решением уравнения. Элемент ab-1 обозначается символом a/b.
Теорема: пусть F=<F,+,-,*,1> - поле. Тогда для любых элементов a, b, c поля:
1) если ab=1, то a0 и b=a-1;
2) если ac=bc b с0 , то a=b;
3) если ab=0, то a=0 или b=0;
4) если a0 и b0, то ab0;
5) a/b=c/d тогда и только тогда, когда ad=bc, b0 и d0;
6) a/b±c/d=(ad±bc)/bd;
7) a/b*c/d=ac/bd;
8) a/b+(-a)/b=0 и –(a/b)=-a/b;
9) если a0 и b0, то (a/b)-1=b/a;
10) ac/bc=a/b
Док-во 1-3:
1) если ab=1, то a0, т.к. при a=0 0*b=1 и 0=1, что в поле невозможно. Поскольку a0, существует элемент a-1, обратный a и b=(a-1a)b=a-1(ab)=a-11=a-1.
2) если ac=bc и c0, то в поле существует элемент с-1 и a=(ac)c-1=(bc)c-1=b, т.е. a=b.
3) из ab=0 следует a=0 или b=0. В самом деле, если a0, то существует элемент a-1 и b=(a-1a)b=a-1(ab)=a-10=0
Поле рациональных чисел. Полем рациональных чисел называется поле частных кольца целых чисел. Элементы поля рациональных чисел называются рациональными числами. Из определения следует, что любое рациональное число можно представить в виде частного целых чисел. Отметим, что любое поле, изоморфное полю рациональных чисел, также является полем рациональных чисел. Отношение порядка на множестве Q рациональных чисел вводится с помощью отношения порядка < на множестве Z целых чисел.
Отношение < на множестве Q рациональных чисел определяется следующим образом: для любых двух рациональных чисел p/q и r/s, где p, rZ и q, sN\{0}, p/q<r/s тогда и только тогда, когда ps<qr.
Теорема: бинарное отношение < на множестве Q рациональных чисел обладает следующими свойствами:
1)для любых a, b, c из Q если a<b и b,c, то a<c;
2) для любых a, b из Q имеет место одно и только одно из трех соотношений: a<b, a=b, b<a;
3) для любых a, b, c из Q, если a,b, то a+c<b+c;
4) для любых a, b, c из Q, если a<b и 0<c, то ac<bc.
Упорядоченное поле. Пусть F— алгебраическое поле и для его элементов определён линейный порядок, то есть задано отношение ≤ со следующими свойствами:
1.Рефлексивность: x≤x
2.Транзитивность: если x≤y и y≤z, то x≤z
3.Антисимметричность: если x≤y и y≤x, то x=y
4.Линейность: все элементы F сравнимы между собой, то есть либо x≤y, либо y≤x
5. Если x≤y, то для любого z: x+z≤y+z.
6. Если 0≤x и 0≤y, то 0≤xy.
Если все 6 свойств выполнены, то поле F называется упорядоченным.
Дата добавления: 2015-07-30; просмотров: 5704;